4.4.2 Развитие нейросетевых моделей

В целом на первый взгляд, модель Мак-Каллока и Питтса порождала больше вопросов, чем давала ответов. Но всё же это было куда лучше, чем отсутствие даже вопросов. Вопрос побуждает кого-то задуматься над ответом на него, а удачные ответы двигают науку и технологии вперёд. У Мак-Каллока и Питтса нашлось немало последователей, желающих улучшить исходную модель или даже предложить новую.

В развитии нейросетевых моделей в 1950-е гг. можно выделить два принципиально разных подхода: монотипический и генотипический. В рамках монотипического подхода свойства нейронов задаются изначально, а топология сети полностью фиксирована. Собственно, монотипический подход эквивалентен обычному программированию, в котором роль программы выполняет конструируемая создателем нейронная сеть. Символьные модели нейронных сетей, подобные модели Мак-Каллока и Питтса, точно так же, как и языки программирования, основаны на формальной логике.

Альтернативой монотипическому стал генотипический подход. При его использовании свойства элементов сети могут быть полностью определены, но параметры этих элементов задаются только частично (например, с помощью набора ограничений и параметров вероятностных распределений). При использовании генотипического подхода описание сети соответствует по сути не отдельному её экземпляру, а целому классу возможных сетей, обладающих заданными свойствами. Это различие в подходах приводит к важным различиям в типах создаваемых моделей и в том, как их можно применять. Например, в случае монотипических моделей можно применять бинарную алгебру логики (высказываний), а вот теория вероятностей плохо подходит для анализа качества работы такой системы. Статистика и теория вероятностей предназначены для анализа множеств объектов или событий и малополезны в случае изучения свойств системы с детерминированным поведением. Конечно, мы можем сделать вывод о том, решает или не решает данная сеть поставленную перед ней задачу. Однако если мы принимаем принцип «либо да, либо нет», то с точки зрения вероятностного подхода задача превращается в абсурдный анекдот: «Какова вероятность встретить на улице динозавра? Пятьдесят процентов: или встретишь, или не встретишь!»

С другой стороны, при работе с генотипическими моделями бинарная алгебра логики может стать неадекватным задаче инструментом. Хотя конкретный экземпляр системы, созданной при помощи генотипического подхода, вполне может быть описан языком формальной логики, наибольший интерес представляют свойства класса систем, порождаемого заданными правилами их построения. Эти свойства лучше всего описывать статистически, поэтому теория вероятностей играет важную роль в генотипическом подходе.

Мы уже упоминали про попытку Питтса применить статистическую механику к нейронным сетям, осуществлённую им под влиянием идей Винера. Вместе с Мак-Каллоком и учеником Рашевского Гербертом Лэндалом Питтс в 1943 г. опубликовал в «Бюллетене математической биофизики» работу «Статистическое следствие логического исчисления нервных сетей» (A Statistical Consequence of the Logical Calculus of Nervous Nets). Хотя топология сети в статье полагается по-прежнему неизменной, выдвигается предположение, что нервные импульсы генерируются в нейронах с различными частотами. Авторы вводят понятие «период латентного суммирования» [period of latent addition] — промежуток времени, в пределах которого нервные импульсы на входе нейрона суммируются (или же происходит торможение — в случае получения на этом промежутке времени импульса от нейрона, связанного с нашим нейроном тормозящей связью). Это расширение исходной модели, по мнению авторов, «позволяет нам производить определённые предсказания количественных характеристик ответа на основе количественных характеристик стимула. Эти предсказания можно сравнивать с наблюдениями и, если необходимо, изменять сети до тех пор, пока последующие предсказания не будут подтверждены».

В некотором смысле эта процедура напоминает обучение искусственной нейронной сети, хотя в действительности авторы работы формулируют несколько иную цель, а именно подбор параметров модели таким образом, чтобы её предсказания соответствовали «численно измеримым психическим феноменам», возникающим в результате нервной активности в биологической сети. Словом, речь идёт о создании достоверной модели естественной нейронной сети, а не об обучении искусственной нейронной сети для решения прикладных задач. Кроме того, чётких представлений о конкретных алгоритмах подбора параметров сети у создателей первой модели искусственного нейрона, по всей видимости, не было.

Тьюринг интересовался возможностью моделирования работы нейронных сетей по крайней мере с 1946 г., когда писал в одном из писем к Россу Эшби: «В работе над [компьютером] ACE [Automatic Computing Engine] меня больше интересует возможность создания моделей работы мозга, чем использование машины для прикладных вычислений. <…> Хотя мозг в действительности может работать, изменяя свои нейронные цепи за счёт роста аксонов и дендритов, мы, однако, могли бы создать модель внутри ACE, позволяющую нам делать то же самое без изменения существующей конструкции ACE, изменяться будут только хранящиеся в памяти машины данные…»^,

В неопубликованной работе под названием «Мыслящие машины» (Intelligent Machinery), написанной в 1948 г., Тьюринг описал сети нейроноподобных логических элементов, названных им «неорганизованными машинами» [unorganized machines].

Машины типа A, описанные в статье, состоят из случайно соединённых логических элементов, каждый из которых имеет два входа и один выход. Логические элементы имеют два состояния — 0 или 1. Это состояние в момент срабатывания элемента определяется при помощи логического вентиля «И-НЕ» — такие вентили называют также NAND-вентилями или элементами Шеффера в честь американского математика и логика Генри Шеффера, который в 1913 г. доказал, что функция «И-НЕ» (инверсия конъюнкции) является универсальной, которой можно заменить все другие логические функции.

Последовательностью срабатывания элементов управляет синхронизирующее устройство, подключенное к каждому из элементов. Это устройство через определённые интервалы времени одновременно посылает сигналы всем элементам, вызывая их срабатывание.

Тьюринг отметил, что последовательность внутренних состояний такой машины будет носить циклический характер, при этом длина цикла будет не более 2^N, где N — число элементов в машине.

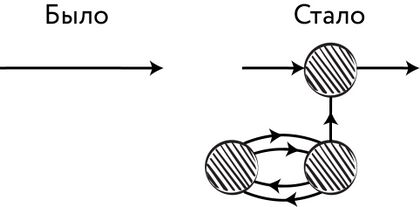
Затем Тьюринг предложил модификацию машины типа A, при которой в каждую связь «И-НЕ» между двумя элементами добавляется сеть из трёх элементов (где все связи тоже типа «И‑НЕ»):

Рис. 89. Предложенная Тьюрингом модификация связей машины типа A

Такая сеть выполняет роль модификатора сигнала. Несложно заметить, что в результате соединение может — в зависимости от значений, помещённых в «нижние» ячейки модификатора (две единицы, два нуля, ноль и единица), — приобрести три возможных типа поведения соответственно: 1) оно будет инвертировать проходящий через него сигнал, то есть заменять 1 на 0, а 0 на 1; 2) оно будет превращать все сигналы в 1; 3) оно будет чередовать поведение (1) и (2) в чётные и нечётные моменты времени. Машина с такими модификаторами соединений получила у Тьюринга название «машина типа B». Все машины типа B являются в то же время и машинами типа A, но не все машины типа A являются машинами типа B.

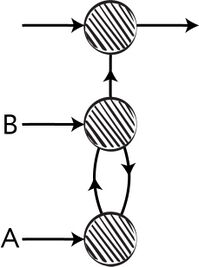
В целом сети Тьюринга напоминают сети Мак-Каллока и Питтса: даже использование цикла в качестве механизма памяти для хранения состояния модификатора отсылает нас к рассуждениям Питтса. Однако Тьюринг делает два важных шага вперёд. Во-первых, он рассматривает возможность моделирования работы сети на программном уровне при помощи электронной вычислительной машины общего назначения. А во-вторых, в его статье содержится целый раздел, посвящённый машинному обучению или, как называет его сам Тьюринг, «образованию машин» [Education of Machinery]! Для этого он анализирует возможные способы «организации неорганизованных машин». Тьюринг вносит изменение в архитектуру модификатора соединения, снабжая его двумя внешними входами.

Рис. 90. Предложенное Тьюрингом изменение архитектуры модификатора соединения

Таким образом, работа соединения становится управляемой: подавая на входы A и B разные сигналы, можно добиться переключения поведения модификатора.

По словам Тьюринга, благодаря применению «соответствующих вмешательств, имитирующих обучение [education]», машина может быть обучена «выполнять любую требуемую работу при наличии достаточного времени и при условии достаточного количества элементов».

Тьюринг рассуждает о том, что настройка машины для выполнения конкретной операции может производиться как вручную, так и на основе системы подкреплений и штрафов, соответствующих удовольствию и боли у живых организмов. При этом сами принципы функционирования сети достаточно просты — в живой природе они могут быть описаны сравнительно небольшим набором генов, благодаря чему такие принципы могут быть выработаны в процессе эволюции. Некоторые исследователи считают, что в этих рассуждениях Тьюринг предвосхитил появление генетических алгоритмов, то есть алгоритмов, имитирующих процессы естественной изменчивости, скрещивания и отбора для решения различных задач оптимизации. Сегодня машины типа A и машины типа B часто называют нейронными сетями Тьюринга или просто сетями Тьюринга.

Тьюринг не приводит конкретных алгоритмов обучения машин типа B, замечая, что обучение таких машин слишком сложный процесс для того, чтобы его можно было смоделировать при помощи бумаги и карандаша, однако приводит пример более простой машины (машина типа P), которая первоначально обладает случайным поведением, выдавая случайные ответы на все запросы. Если ответ окажется правильным, машина запомнит, что в такой ситуации следует дать именно этот ответ (положительное подкрепление). Если же ответ окажется неправильным, машина, напротив, запомнит, что в этой ситуации именно этот ответ давать не следует. Тьюринг ограничивается описанием принципа работы машины, опуская детальное описание её архитектуры^, .

Причина, по которой работа Тьюринга не была опубликована, довольно забавна. Можно сказать, что она пала жертвой отбора. Начальник Тьюринга по имени Чарльз Дарвин, внук знаменитого основоположника теории эволюции, отозвался о статье Тьюринга в критическом ключе, заявив, что по своему качеству она ничем не лучше школьного сочинения.

Между тем исследования в области искусственных нейронных сетей продолжались. В 1948 г. Альфонсо Шимбел и Анатоль Рапопорт из Чикагского университета описали семейство статистически организованных сетей. Отталкиваясь от модели Мак-Каллока и Питтса, Шимбел и Рапопорт рассмотрели различные параметры нейрона и его компонентов в качестве случайных величин, имеющих некоторые вероятностные распределения. Из них они вывели общее уравнение для расчёта вероятности того, что нейрон в указанном месте сработает в указанное время.

Loading comments...