3.4.2 Продолжение. Шашечная программа Артура Сэмюэла

Программа, описанная Сэмюэлом в статье 1967 г., отличается от программы Стрейчи примерно так же, как ВАЗ-2101 («копейка», которую, к слову, начали производить тремя годами позже) от крестьянской телеги. В программе Сэмюэла уже можно разглядеть многие черты современных шашечных и шахматных программ.

Для начала Сэмюэл выбрал для оценки обычных шашек и дамок величины, относящиеся друг к другу как 3 : 4, что более точно соответствовало человеческим экспертным знаниям. Помимо подсчёта шашек и дамок на доске, Сэмюэл добавил в оценочную функцию множество позиционных факторов. Например, учитывались мобильность (количество потенциальных ходов у каждого из игроков без учёта взятий) и контроль каждой из сторон над различными участками поля. Сама игра была разделена на шесть стадий, в каждой из которых значения оценок каждого из факторов могли быть разными. Кроме того, оценочная функция Сэмюэла учитывала сочетания некоторых факторов, а также тот факт, что в зависимости от очерёдности хода эти сочетания могут иметь различную оценку. В результате итоговая оценочная функция имела более 10 000 параметров. Хотя Сэмюэл и использовал фиксированный набор факторов, он замахнулся ещё и на автоматический подбор их значений. Действительно, установить значения для такого внушительного набора параметров экспертным путём представлялось малореальным.

Однако для автоматической подстройки нужна была обучающая выборка. Для того чтобы её создать, примерно 250 000 позиций из игр шашечных мастеров было выбито на перфокартах, а затем перенесено на магнитную ленту. Для каждой позиции был отмечен ход, сделанный игроком (использовались только позиции с ходами не проигравших партию игроков). Затем Сэмюэл использовал весьма нетривиальную процедуру, включающую специальные способы сглаживания значений параметров, для подбора таких их значений, чтобы при переборе на один полуход в глубину его программа как можно чаще «угадывала» ходы, сделанные мастерами (в случае взятий глубина перебора могла увеличиваться). Сеанс обучения длился около десяти часов.

Для оценки качества предсказания Сэмюэл использовал простую метрику, напоминающую коэффициент корреляции: C = (L – H) / (L + H), где L — суммарное количество всех возможных ходов, которые программа оценила ниже, чем «правильный» ход, сделанный мастером, H — суммарное количество всех возможных ходов, которые программа оценила выше, чем ход, сделанный мастером. Таким образом, при полном угадывании программой ходов мастера метрика C будет равна «1», при полном неугадывании — «–1», а при случайной оценке ходов — «0».

Хотя отдельные ходы мастеров могли быть ошибочными либо имели равные им по силе альтернативы, Сэмюэл считал, что при достаточно большом объёме выборки это не будет являться серьёзной проблемой. В результате экспериментов по подстройке параметров автору удалось получить значение C = 0,26 при использовании оценочной функции, учитывающей значение каждого из факторов по отдельности, и C = 0,48 для функции, использовавшей сочетания факторов. По оценке Сэмюэла, подобранные параметры позволяли программе при переборе в глубину на один полуход в 64% случаев ставить ход мастера по оценке на первое или второе место.

Радикальным образом изменился и механизм перебора вариантов. Внимательные читатели наверняка заметили один из очевидных изъянов программы Стрейчи — фиксированную глубину анализа вариантов. Представим, что перебор ограничен глубиной в два полухода и производится в позиции с равным количеством шашек, а вторым полуходом оказалось взятие соперником нашей шашки. Оценочная функция, рассматривая позицию, возникшую после взятия, даст ей отрицательную оценку — действительно, в этой позиции у противника появилось преимущество в шашку. Однако взятие на самом деле может быть началом банального размена, и уже на следующем полуходе взятая шашка отыгрывается обратно. Но машина этого «не видит», потому что исчерпан лимит глубины перебора. Эта проблема сегодня широко известна под названием «эффект горизонта». Сэмюэл боролся с ней, позволяя программе прерывать перебор только в узлах дерева, в которых нет взятий.

Ещё одним радикальным нововведением стало применение так называемого альфа-бета-отсечения. Этот метод был в нескольких разных модификациях независимо открыт и развит в разное время целым рядом исследователей. К их числу относятся Джон Маккарти, который впервые выдвинул идею на ставшей впоследствии знаменитой Дартмутской конференции 1956 г.; Аллен Ньюэлл, Герберт Саймон и Клифф Шоу, описавшие в 1958 г. алгоритм перебора шахматной программы, использующей односторонний вариант альфа-бета-отсечения; Александр Брудно, в 1963 г. независимо от американцев разработавший этот метод (под названием «метод граней и оценок») и формально доказавший его корректность; Джеймс Слейгл, Филип Бурский, Джон Диксон и сам Сэмюэл, которые описали метод в своих статьях конца 1960-х, и, наконец, Дональд Кнут и Рональд Мур, уточнившие определение и посвятившие альфа-бета-отсечению в 1974 г. отдельное объёмное исследование.

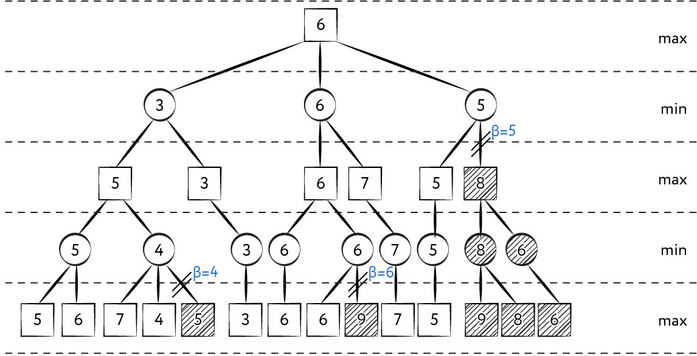
Основная идея метода заключается в том, что в некоторых случаях нам не нужно знать точную оценку того или иного варианта в дереве перебора, достаточно лишь установить, что эта оценка выше или ниже определённой границы. Например, программа проанализировала некоторый ход X в определённой позиции и обнаружила, что он приводит к выигрышу шашки. Анализируя альтернативный ход Y, она обнаруживает, что у противника есть ответный ход, который приводит к ничейной позиции. В таком случае анализ всех остальных возможных ответов противника на ход Y избыточен: да, может быть, у противника есть ещё более сильный ответ, который, например, приводит к потере машиной шашки, но это уже совершенно не важно, ведь ход Y уже был опровергнут. Верхняя граница оценки (beta) для одного игрока является взятой с противоположным знаком нижней границей оценки (alpha) для второго игрока, и наоборот. Таким образом, процедура перебора получает в качестве параметров величины alpha и beta и осуществляет поиск внутри «окна», задаваемого этими параметрами. Если в ходе перебора машине всегда везло и первый рассмотренный ход в каждом из узлов дерева перебора оказывался действительно сильнейшим, то вместо рассмотрения N позиций в ходе перебора нам потребуется рассмотреть их только около $\sqrt{N}$, что является весьма существенным достижением. Конечно, на практике упорядочить ходы-кандидаты идеальным образом не получится, но за последние полвека создатели шахматных и шашечных программ придумали множество остроумных алгоритмов, позволяющих эффективно выявлять наиболее перспективные ходы-кандидаты. Например, можно использовать перебор вариантов с сокращённой глубиной, чтобы выявить самый потенциально сильный ход, как это делал Сэмюэл. Важно отметить, что альфа-бета-отсечение является полностью корректным, то есть гарантирует получение той же самой оценки в корне дерева перебора, что и алгоритм полного перебора вариантов без отсечений.

Рис. 62. Пример работы альфа-бета-отсечения

Помимо альфа-бета-отсечения, программа Сэмюэла использовала и набор весьма оригинальных эвристических отсечений.

И наконец, программа Сэмюэла использовала метод обучения, названный «зубрёжка» (rote learning) и заключавшийся в запоминании оценок позиций, уже встречавшихся в предыдущих партиях. Встретив такую позицию в нижних узлах дерева перебора, программа повторно использовала оценку, полученную в прошлый раз в результате более глубокого перебора, что позволяло не только сэкономить время, но и получить более надёжную оценку (поскольку глубина перебора в прошлый раз была больше, то меньше была и вероятность ошибки), избежав, возможно, ошибки, сделанной в предыдущий раз. Учитывая, что дебюты и окончания шашечных партий часто повторяются, этот метод был достаточно эффективен.

Одной из целей создания программы Сэмюэла стала необходимость тестирования нового компьютера. Будучи сотрудником компании IBM, Сэмюэл предположил, что программа для игры в шашки может послужить удобным инструментом проверки полноты и эффективности набора инструкций, предлагаемых для машины IBM 701, в разработке которой он принимал участие.

Работа над IBM 701 привела среди прочего к появлению одного из фундаментальных компьютерных алгоритмов — метода, называемого сегодня хешированием. Благодаря Сэмюэлу и его коллегам современные компьютерные программы могут быстро заносить данные в таблицы и столь же быстро извлекать их оттуда.

Спустя три десятилетия Сэмюэл так описывал свою работу: «В те дни IBM не слишком хорошо относилась к тому, что один из их инженеров тратит рабочее время на игру в шашки, пусть даже и против машины, поэтому большую часть моей работы по шашкам приходилось выполнять в свободное время. Я придал своей работе некоторую степень респектабельности, снабдив программу функцией обучения, но даже тогда только использование программы в качестве непрерывно работающего средства тестирования компьютера позволяло мне получать машинное время, необходимое для проверки моих экспериментальных обучающих процедур».

24 февраля 1956 г. программа Сэмюэла была впервые публично продемонстрирована в телевизионной передаче. Перед этим Томас Уотсон — старший, тогдашний президент IBM, организовал показ программы акционерам^, .

В 1961 г. Эдвард Фейгенбаум и Джулиан Фельдман, работавшие над первым фундаментальным трудом, обобщавшим результаты исследований в области ИИ под названием «Компьютеры и мысль» (Computers and Thought), попросили Сэмюэла предоставить для сборника статью о методах, используемых в его программе. Одним из пожеланий было наличие приложения к статье, в котором обсуждалась бы лучшая из партий, сыгранных программой. Сэмюэл решил, что лучшим способом добыть такую партию будет организация матча с каким-либо сильным шашистом. В качестве соперника был выбран Роберт Нили. IBM Research News утверждала, что Нили был «чемпионом Коннектикута по шашкам и одним из ведущих игроков страны». История с партиями программы Сэмюэла против Нили — один из увлекательных детективных эпизодов истории ИИ. Нили, по всей видимости, был лишь чемпионом Коннектикута среди незрячих игроков. Более того, в 1962 г. он завоевал титул чемпиона США среди незрячих игроков в турнире, организованном Американской шашечной федерацией (American Checkers Federation, ACF). Однако титул он получил по причине неявки других игроков — у Нили попросту не нашлось ни одного противника. Первый соперник появился у Нили только год спустя, в турнире 1964 г. (уже на звание чемпиона мира среди незрячих игроков!), когда Нили удалось отстоять титул в матче из четырёх партий. В ряде источников утверждается также, что Нили был мастером, однако Джонатану Шефферу не удалось обнаружить подтверждений наличия у Нили этого звания.

Были ли основания утверждать, что Нили — «один из ведущих игроков страны»? Современный анализ партии, проигранной Нили программе Сэмюэла, показывает, что обе стороны совершали ошибки и, по мнению Шеффера, ошибки, допущенные Нили, были слишком грубы для «одного из ведущих игроков страны».

Программа выиграла, и это произвело эффект разорвавшейся бомбы. Интеллектуальное превосходство человека оспаривается электронными монстрами! Компьютеры появились лишь недавно, но уже превзошли человека в шашках! Скоро они превзойдут его и во всём остальном! Словом, для невежественной публики 1962 г. это стало крупным событием. Даже тот факт, что год спустя Нили выиграл у программы Сэмюэла в мачте из шести партий, победив в одной и завершив вничью пять остальных, уже не мог остановить распространение соответствующих настроений в обществе.

В 1966 г. Сэмюэл взял свою программу на матч за звание чемпиона мира между Уолтером Хеллманом (действующим чемпионом из США) и британским претендентом Дереком Олдбери. IBM выступила спонсором мероприятия при условии, что участники сыграют несколько партий с программой Сэмюэла. Было сыграно четыре игры против каждого соперника, и все они окончились поражением программы. Стало ясно, что ожидания были несколько завышенными.

Лишь спустя десятилетие появилась действительно сильная шашечная программа, она была написана в Университете Дьюка Эриком Дженсеном и Томом Траскоттом при поддержке доктора Алана Бирмана. Изначально программа называлась Duke, но затем была переименована в Paaslow. Новое имя программа получила в честь персонажа одного из скетчей Монти Пайтона — мистера Пасло (Paslow). Дженсен записал имя персонажа на слух, удвоив букву А, чтобы подчеркнуть правильный вариант произношения (в скетче имя произносится именно с долгим [а:]), подобно тому как это сделано в названии государственного образования Синт-Мартен (Sint Maarten). Спустя много лет Дженсен расстроился, когда обнаружил, что в сценарии скетча имя этого безголового персонажа было записано как Paslo, без буквы W на конце. Впрочем, современные варианты сценария, доступные в Сети, придерживаются варианта Paslow, что делает резонным вопрос о том, знает ли кто-то теперь, какой именно вариант правильный.

В качестве аппаратной платформы проекта разработчики использовали мощный для того времени компьютер IBM 370. Поскольку Дженсен и Траскотт не были опытными игроками в шашки, то при создании оценочной функции они ориентировались на работы Сэмюэла. В то же время у разработчиков был опыт создания одной из сильнейших шахматных программ своего времени, что, по всей видимости, оказалось в данном случае решающим — в 1977 г. программа Дженсена и Траскотта выиграла всухую матч из двух игр против программы Сэмюэла. Затем состоялся демонстрационный матч из пяти игр с гроссмейстером Элбертом Лаудером, в котором программа смогла выиграть одну партию, проиграла две и две оставшиеся завершились вничью. Причём в партии, выигранной программой, она в какой-то момент находилась в проигранной позиции, но затем Лаудер совершил ошибку и умудрился проиграть.

Хотя некоторые авторы и считали, что «люди не могли сравниться с Paaslow», шашечные эксперты не разделяли столь безудержного энтузиазма, и дело было даже не в том, что Лаудер выиграл этот небольшой матч.

Известный эксперт в области шашек и многократный чемпион Иллинойса Ричард Фортман, комментируя игру Duke против программы Сэмюэла, писал: «Игра в окончании, особенно во второй игре, была ужасной. Должен сказать, что в настоящее время есть несколько тысяч средних игроков-второразрядников [class B players], которые могут без проблем победить любой компьютер». Уильям Гранжан, секретарь Американской шашечной федерации, прокомментировал качество игры так: «Мнение доктора Бирмана, что программа Duke близка к статусу чемпиона мира, — смехотворно».

Команда Университета Дьюка тем не менее была вдохновлена своими успехами и желала бросить вызов чемпиону мира — доктору Мариону Тинсли. Последний, заручившись поддержкой Американской шашечной федерации, предложил открытое пари на сумму 5000 долларов сроком на пять лет, утверждая, что победит любую шашечную программу. К сожалению, авторам программы не удалось собрать необходимую сумму денег: 5000 долларов в 1977 г. были весьма внушительной суммой, эквивалентной более 25 000 долларов 2023 г. Надежда привлечь внимание национального телевидения также провалилась. Программа Дженсена и Траскотта с этого момента не сыграла ни одной публичной партии, и работа над ней была прекращена.

Удивительно, но чрезмерно оптимистичное освещение успехов первых шашечных программ имело отрицательный эффект. Оптимизм Сэмюэла, многократно усиленный прессой, привёл к распространению заблуждения о том, что шашки были «решены», или по крайней мере о том, что компьютерные программы бесповоротно превзошли человека в этой игре. Отчасти здесь сыграла роль, по всей видимости, иллюзорная простота шашек — ведь по сравнению с шахматами в них всего два вида фигур, да и перемещаться они могут лишь по чёрным клеткам доски. Многие научные и научно-популярные книги и статьи упорно плодили заблуждения, и даже пари, объявленное Тинсли, не смогло переломить силу многократно растиражированного невежества.

Со времён Paaslow и до 1989 г. в области компьютерных шашек царило затишье, а когда в 1992 г. Джонатан Шеффер, встретившись на одной из конференций с членом Совета естественных наук и инженерии Канады (NSERC), основного агентства финансирования научных исследований в стране, поинтересовался, почему прошлогодний запрос на финансирование исследований ИИ с использованием шашек в качестве экспериментального испытательного стенда был отклонён, то получил ответ: «А разве Сэмюэл не решил эту игру ещё тридцать лет назад?»

‎

Loading comments...