3.4.1 Начало. Шашечная программа Кристофера Стрейчи

Создание первой компьютерной программы для игры в шашки часто приписывают Артуру Сэмюэлу. Однако в действительности приоритет в этой области принадлежит, по-видимому, другому программисту — Кристоферу Стрейчи, что признавал и сам Сэмюэл. Вот что он писал по этому поводу:

Стрейчи действительно заинтересовался шашками довольно рано, хотя, возможно, не в 1947 году, когда я начал работать над своей программой в Университете Иллинойса. Тем не менее Чарльз Бэббидж <…> ещё раньше предлагал использовать свою «аналитическую машину» для игры в шашки и шахматы, так что Бэббидж в любом случае опередил нас обоих. Моя первая программа для игры в шашки для компьютера Illiac Иллинойсского университета так и не была ни разу запущена, потому что Illiac существовал только на бумаге, когда я покинул этот университет, чтобы перейти на работу в IBM в 1949 году. Только в 1952 году моя программа заработала на экспериментальной модели компьютера IBM 701. Кстати, эта первая программа была написана в машинных кодах (набор кодов операций конкретной вычислительной машины. — С. М.) — ещё до того, как у нас появился символьный ассемблер.

Я узнал о работе Стрейчи из статьи, которую он представил в Торонто в сентябре 1952 года. Поскольку его программа в то время уже была опубликована, я должен признать своё поражение. Только в 1954 году, с появлением IBM 704, моя программа смогла продемонстрировать интересную игру. Мой вклад заключался в добавлении «обучения» в программу, и я считаю, что могу претендовать на приоритет в этом вопросе.

Рис. 59. Портрет Кристофера Стрейчи, отпечатанный при помощи компьютера, хранящийся в Бодлианской библиотеке Оксфордского университета

Первая версия программы Стрейчи для прототипа британского компьютера ACE (Automatic Computing Engine) была завершена в феврале 1951 г., однако объёма оперативной памяти машины оказалось недостаточно для полноценной работы программы.

Когда Стрейчи услышал о машине Manchester Mark 1, обладавшей значительно большим объёмом памяти, он попросил у бывшего сокурсника по Кингс-колледжу Кембриджа Алана Тьюринга руководство по программированию этой машины и к октябрю 1951 г. перевёл свою программу в машинный код для Manchester Mark 1 (коммерческая версия этой машины получила название Ferranti Mark 1) — иногда эту машину называют MADM (Manchester Automatic Digital Machine, Манчестерская автоматическая цифровая машина) или даже MADAM. Летом 1952 г. программа могла «сыграть полноценную партию в шашки на разумной скорости».

Стрейчи был также одним из пионеров компьютерной музыки. В руководстве по программированию, полученному Стрейчи от Тьюринга, упоминается инструкция, позволяющая передавать импульсы на встроенный динамик компьютера. Тьюринг пишет, как, управляя паузами между импульсами, можно производить звуки разной высоты. Тьюринг рекомендует использовать эту инструкцию для оповещения оператора машины об определённых событиях. Стрейчи сделал следующий шаг, научив машину исполнять несколько мелодий: британский гимн (God Save the King — дело было ещё при жизни Георга VI), Baa Baa Black Sheep и In the Mood. В 1951 г. мелодии были записаны вещательным подразделением Би-би-си. В 2016 г. исследователи из Университета Кентербери восстановили мастер-диск и загрузили записанные на него мелодии в облачный сервис Soundcloud^, . Таким образом, мелодии, созданные Стрейчи, стали первой дошедшей до нас компьютерной музыкой. Если бы Стрейчи чуть поторопился, то, возможно, его компьютерная музыка стала бы и первым в мире образцом компьютерной музыки, но его опередил Джеффри Хилл, научивший чуть раньше австралийский компьютер CSIR Mk1 воспроизводить «Марш полковника Боги» (Colonel Bogey March).

Но, так или иначе, шашечная программа Стрейчи не просто научилась играть в шашки раньше программы Сэмюэла, но и исполняла в конце партии британский гимн.

В сентябре 1966 г. текст программы Стрейчи, переписанной на изобретённом им высокоуровневом языке программирования CPL, был опубликован в специальном выпуске журнала Scientific American, посвящённом информации. В 2011 г. Питер Норвиг реализовал простой транслятор с языка CPL на Python и, устранив несколько опечаток, смог вернуть программу Стрейчи «к жизни».

Если взглянуть на начальную позицию в английских шашках, легко заметить, что белые могут начать партию одним из семи возможных полуходов (полуход, по-английски ply, возможно сокращение от reply — ответ, — перемещение шашки одного из цветов, ход — два последовательных полухода за белых и за чёрных), на каждый из которых чёрные могут также ответить семью возможными ответными полуходами. Таким образом, в результате первого полухода на доске может возникнуть семь позиций, в результате двух последовательных полуходов — 49 позиций. Далее число возможных полуходов меняется, и после трёх полуходов на доске может возникнуть 302 позиции, но некоторые из них будут повторяться, поскольку возникнут в результате перестановок ходов, и уникальных позиций будет всего 216. Современные шашечные программы умеют учитывать подобные повторения, запоминая часть проанализированных позиций в оперативной памяти, но в начале 1950-х оперативная память Ferranti Mark 1 позволяла хранить всего 512 чисел, по 20 бит каждое, поэтому о таких изысках, как таблица перестановок, не приходилось и мечтать. С увеличением количества полуходов число их возможных цепочек растёт очень быстро: 5 полуходов — 7361 вариант (уникальных позиций — 2733), 6 полуходов — 36 768 вариантов (уникальных позиций — 9105), 7 полуходов — 179 740 вариантов (уникальных позиций — 28 123) и так далее. При 28 полуходах мы получим астрономическое число 16 377 718 018 836 900 735 вариантов. Современному компьютеру, способному просматривать 10 млн вариантов в секунду, потребовалось бы на их рассмотрение почти 52 000 лет, а ведь речь идёт лишь о партиях не длиннее 14 ходов. Совершенно очевидно, что перебор необходимо каким-то образом ограничить. Программа Стрейчи способна просматривать дерево вариантов игры на фиксированное число полуходов. При этом, поскольку позиции в терминальных узлах дерева в ряде случаев ещё далеки от завершения игры, Стрейчи использовал вместо неизвестной точной оценки позиции приближённую, выбрав в качестве приближения разницу в числе своих шашек и шашек противника (дамка оценивалась в четыре шашки). Функцию, выполняющую такую приближённую оценку позиции, сегодня принято называть оценочной функцией [evaluation function]. Подчёркивая неточный, основанный на предположениях и догадках характер заложенного в них знания, подобные функции называют эвристическими (от др.-греч. εὑρίσκω — отыскиваю, открываю). Действительно, хотя позиции, в которых у одной из сторон есть преимущество в числе шашек, часто являются выигрышными для этой стороны, но из такого правила несложно найти множество исключений.

Примечательно, что с математической точки зрения оценочная функция, выбранная Стрейчи, является полиномом: f = M_c – M_p + 4K_c – 4K_p, где M_c — число шашек машины, M_p — число шашек противника, K_c — число дамок машины, K_p — число дамок противника. Все позиции в шашках, согласно теореме Цермело, должны быть либо выигрышными, либо проигранными, либо ничейными при идеальной игре обеих сторон. В примере с крестиками-ноликами мы использовали для выигрышной позиции оценку «1», для ничейной — «0» и для проигрышной — «–1». Такая оценка очевидным образом связана с числом очков, которое игрок получит при соответствующем результате, s = (v + 1) / 2, где s — число очков, а v ∈ {−1, 0, 1} — оценка, которую мы использовали в крестиках-ноликах. Оценка со знаком позволяла нам легко получить значение оценки для противника, достаточно было просто поменять у оценки знак: v_c = –v_p, вместо того чтобы выполнять менее наглядную операцию вычитания оценки из единицы: s_c = 1 – s_p, но это в некоторой степени дело вкуса.

В случае эвристической оценки мы в подавляющем большинстве случаев не уверены в её точности. Из-за этой неуверенности оценка приобретает вероятностный характер. Казалось бы, разумно использовать в качестве оценки математическое ожидание количества очков: s ∈ [0; 1], s = 1 × p(W) + 0,5 × p(D), где p(W) — вероятность победы, p(D) — вероятность ничьей, а для удобства можно было бы преобразовать оценку к виду v ∈ [–1; 1], чтобы работал трюк с переменой знака. Однако вместо этого создатели первых шашечных и шахматных программ выбрали на первый взгляд весьма неудобную полиномиальную форму оценки f, где она может принимать большие по модулю положительные и отрицательные значения. Получается, что позиция, в которой у машины все 12 шашек стали дамками, а у противника не осталось ни одной шашки, будет иметь оценку, равную, например, 48, а если бы дамки оценивались не в 4 единицы, а в 40, то мы получили бы число 480. Но каков смысл этого числа? Каким образом оно связано с ожидаемым результатом партии?

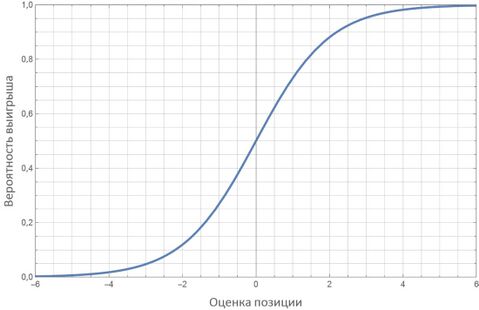
На самом деле такая аддитивная оценка, безусловно, связана с вероятностью победы каждой из сторон. Если бы мы взяли программу Стрейчи и заставили её разыграть астрономическое количество случайных позиций, а затем построили график, в котором по оси x отложили оценку позиции f, а по оси y — среднее количество очков, набранных в играх, начатых с позиции с оценкой x, то получили бы график, напоминающий график логистической функции: s(x) = 1 / (1 + e^–kx), где k — некоторый масштабный коэффициент, e — основание натурального логарифма.

Рис. 60. График зависимости вероятности выигрыша от оценки позиции

То есть выбранный Стрейчи способ оценки всё-таки был связан с вероятностью победы, хотя и неочевидным образом. Но к чему такие сложности, почему бы не использовать в качестве оценки собственно вероятность?

Всё дело в том, что именно такой способ оценки позиции, при котором мы просто представляем её в виде суммы оценок каждого взятого по отдельности признака, является более привычным для людей. В любом шашечном или шахматном учебнике вы найдёте способы оценки, сформулированные именно в таком виде. Например, шахматный учебник скажет, что слон и конь сто́ят примерно по три пешки, ладья — пять, а ферзь — девять. Такой способ оценки позиции является частью старинной традиции. Ещё итальянские шахматные мастера XVII–XVIII вв. пытались оценить «стоимость» фигур в пешках, а их последователи стали аналогичным образом оценивать и различные позиционные факторы. В шашках тоже удобно принять за эталон «стоимость» одной шашки и исчислять «стоимость» дамки, а также различных позиционных элементов оценки, сравнивая их с принятым эталоном. В XX в. машины учились играть в игры у людей и не слишком часто преподавали уроки людям, поэтому и развитие ИИ было в очень большой степени основано на человеческих экспертных знаниях. В 1967 г. Сэмюэл так охарактеризовал современное ему положение вещей: «…при нынешнем уровне развития знаний единственным практическим подходом будет, даже при наличии помощи со стороны цифрового компьютера, разработка эвристик, основанных на копировании (тут автор применяет глагол to ape, т. е. дословно «собезьянивании». — С. М.) поведения человека».

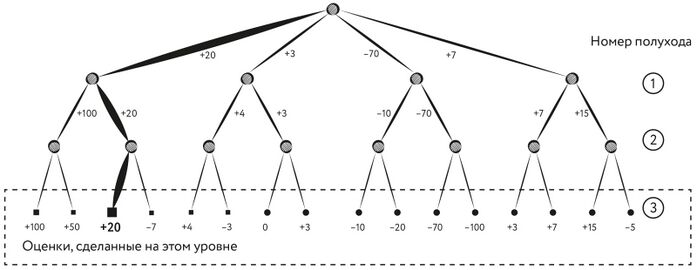
Итак, программа Стрейчи стремилась выбрать ход, который максимизировал бы значение оценочной функции при наилучших ответных действиях оппонента. Такой метод обычно называют минимаксом, поскольку, рассматривая собственные ходы (на нечётных уровнях дерева), программа выбирает ход с максимальной оценкой, а рассматривая ходы оппонента (на чётных уровнях дерева), выбирает ходы, минимизирующие оценку. Если на каждом уровне дерева менять знак оценки на противоположный, то можно обойтись одной только максимизацией. Такую модификацию минимакса обычно называют негамаксом.

Рис. 61. Упрощённая диаграмма, показывающая, как оценки поднимаются по дереву возможных ходов, чтобы получить наилучший следующий ход.
Процесс оценки начинается на уровне (3), где машина выбирает ветку с наиболее положительной оценкой. Далее на уровне (2) от противника ожидается выбор ветки с наименьшей оценкой, и на уровне (1) машина выбирает ветку с наибольшей оценкой

Изобретение минимакса часто приписывают фон Нейману, ведь он рассматривается в одной из его ранних работ — «К теории стратегических игр» (Zur Theorie der Gesellschaftsspiele), написанной в 1928 г. В действительности приоритет в данном случае, по всей видимости, принадлежит Сирио Форелю Эмилю Борелю, который сформулировал отдельные положения теории игр раньше фон Неймана и независимо от него. При некоторой фантазии можно говорить и о приоритете Бэббиджа, который предложил похожий алгоритм для выбора хода в крестиках-ноликах. Как бы то ни было, и Борель, и фон Нейман, и Бэббидж отталкивались от окончательных оценок в терминальных узлах дерева перебора, использовать же усечённое дерево и приближённые оценки первым предложил Норберт Винер.

Максимальная скорость перебора, осуществляемого программой Стрейчи в 1950-е гг., могла достигать, по-видимому, нескольких десятков, быть может ста позиций в секунду, что позволяло программе за разумное время анализировать варианты на глубину три-четыре полухода. Конечно, при столь неглубоком анализе вариантов и крайне примитивной оценочной функции рассчитывать на сильную игру программы не приходилось. Стрейчи не уделял особого внимания дальнейшему развитию алгоритмов, заложенных в программу, и следующий этап развития компьютерных шашек был связан уже с программой Сэмюэла.