Перейти к содержанию

2.1.1 Счёты, абак и астролябия

Материал из Охота на электроовец: Большая Книга Искусственного Интеллекта

Одним из самых древних устройств, применяемых людьми не только для сохранения информации, но и для автоматизации операций, производимых с ней, является абак. Обычно этим словом обозначают различные разновидности счётных досок, применявшихся рядом древних культур для арифметических расчётов[1].

Во многих словарных статьях, посвящённых абаку, благодаря, по всей видимости, некритичному копированию текста из «Википедии», можно встретить следующее определение: «Аба́к (др.-греч. ἄβαξ, ἀβάκιον, лат. abacus — доска) — семейство счётных досок, применявшихся для арифметических вычислений приблизительно с V в. до н. э. в древних культурах…»[2]

У читателя, конечно, тут сложится впечатление, что слово «абак» происходит от древнегреческих ἄβαξ, ἀβάκιον, обозначающих доску. Крепкую дубовую или сосновую доску, которой так и хочется огреть незадачливого автора этого определения. Впрочем, ошибка эта весьма распространена[3]: целый ряд словарей утверждает, что ἄβαξ — это доска. В действительности в Древней Греции для обозначения доски использовалось несколько разных слов. Например, если речь шла о дощечке, применяемой для выполнения рисунка, то по-древнегречески она называлась словом πίναξ, то есть «пинакс». От этого слова происходит слово «пинакотека» (помещение для хранения живописных изображений)[4]. В этом слове тот же корень, что и в русском слове «пень»[5]. Другое слово — δοκός — использовалось для обозначения толстых досок либо балок или бревна (которое не замечаешь в собственном глазу); δόρυ, σανίς[6] — всё это в той или иной степени доски, но вот ἄβαξ — это абак как устройство для счёта (правда, у этого слова есть ещё несколько значений, например в архитектуре ἄβαξ — это плита, венчающая колонну (по-русски «абака» — верхняя часть капители)[7], также это слово иногда могло обозначать поднос, туалетный столик, подставку для сосудов[8]). Латинское abacus — это тоже именно абак как устройство для счёта, потому что строительная доска — это axis или lamina, а доска для письма — tabula (помните tabula rasa?). Чтобы отличать абак от подносов и подставок, римляне заимствовали слово из древнегреческого в форме творительного падежа[9]. В общем, авторы словарной статьи про абак рассказали нам, что слово «абак» происходит от слова «абак».

Существует распространённое мнение, что ранние формы абака представляли собой дощечки, припорошённые песком, а само слово ἄβαξ — результат заимствования семитского корня: еврейского ābāq (אבק) (а-вак), обозначающего пыль, либо финикийского abak, обозначающего песок, — конкретные пути заимствования не ясны[10]. Но не все исследователи с этим согласны[11].

В древнегреческом языке песок обозначается словом ἄμαθος («аматос»), отсюда «абакомантия», также известная как «аматомантия» — вид гадания на основе интерпретации узоров в пыли, грязи, иле, песке или золе из недавно умерших[12].

Абак был распространён чрезвычайно широко. К 2700–2300 гг. до н. э. относится появление первого абака у шумеров — доски с колонками, предназначенными для представления величин последовательных порядков шумерской шестидесятеричной системы счисления[13]. Следует отметить изобретательность древних математиков — число 60 удобно тем, что делится без остатка на 2, 3, 4, 5 и 6, что упрощает многие практические операции. По мнению ряда исследователей, шестидесятеричная система счисления возникла в результате наложения более древних пятеричной и двенадцатеричной систем счисления[14], [15]. Пять — это число пальцев на руке, но откуда могла возникнуть двенадцатеричная система? Существует весьма остроумный способ счёта на пальцах одной руки, при котором большой палец указывает на одну из двенадцати фаланг остальных пальцев. Некоторые народы Нигерии, Индии и Тибета используют двенадцатеричную систему счисления в настоящее время[16], [17], [18].

Двенадцатые доли нередко использовались и в Европе. Древнеримская унция составляла 1⁄12 часть либры (меры веса), 12 унций составляют тройский фунт, 1 английский пенни (пенс) равен 1⁄12 части шиллинга, 1 дюйм — 1⁄12 фута и так далее.

Интересно, что преимущества двенадцатеричной системы счисления нашли сторонников в Новое время. В XVIII в. её адептом был французский математик и естествоиспытатель граф де Бюффон[19]. В 1944 г. было создано «Американское двенадцатеричное общество» (The Dozenal Society of America)[20], а в 1959-м — «Английское двенадцатеричное общество» (The Dozenal Society of Great Britain)[21], объединившие сторонников этой системы счисления. Рассудите сами, при помощи двенадцатеричной системы так удобно считать месяцы в году, христианских апостолов, колена Израиля, полутона в октаве, подвиги Геракла, знаки Зодиака, имамов, наследников Мухаммеда в шиизме, ступени колеса Сансары и бог знает что ещё.

Шестидесятеричной системе мы обязаны 60 секундами в минуте, 60 минутами в часе, 360 градусами в полном угле, минутами и секундами в географических координатах.

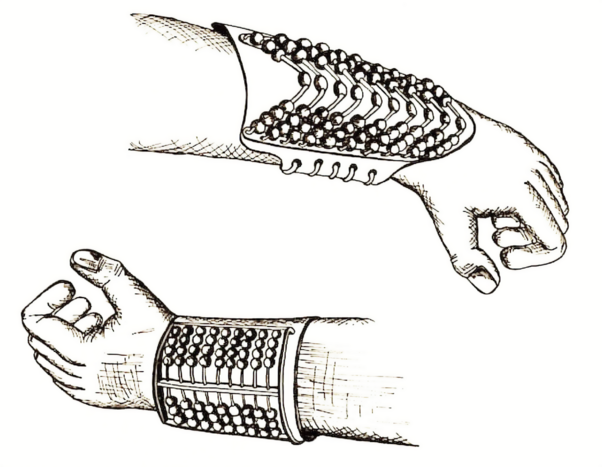
Но вернёмся к абаку. В Древнем мире абак был распространён чрезвычайно широко, и не всегда просто проследить конкретные пути заимствования этой технологии. Вполне вероятно, что счётные приспособления, подобные абаку, изобретались в истории человечества не единожды. На такую мысль наводит, например, информация о существовании сходных приспособлений для счёта в Новом Свете задолго до прибытия туда европейцев. В целом ряде источников о древней математике сообщается, что мезоамериканский абак назывался «непоуальцинцин» [nepoːwaɬˈt͡sint͡sin]. Это слово классического науатля (ацтекского языка) образовано от двух корней: «поуаль» или «поуалли» [ˈpoːwalːi] («счёт») и «цинцин» [t͡sint͡sin] («мелкие одинаковые элементы»). Приставка [ne] в данном случае является определителем существительного, образованного от возвратного глагола[22]. То есть всё в сумме означает примерно «подсчитыватель-при-помощи-фишек». Непоуальцинцин был основан на двадцатеричной системе счисления и иногда выполнялся в форме наручного браслета.

Рис. 8. Непоуальцинцин в форме наручного браслета

Наиболее древние изображения непоуальцинцина относятся к ольмекской культуре (не позднее III в. н. э.).

Рис. 9. Типичный непоуальцинцин (ольмекская культура)

Типичный непоуальцинцин состоял из 13 рядов, каждый из которых насчитывал по семь бусин, разбитых вертикальным разделителем на две группы: в одной из них было четыре бусины, а в другой — три. Первая группа использовалась для обозначения единиц, вторая — для обозначения пятёрок. Число набиралось путём передвижения бусин в направлении вертикального разделителя. Легко заметить, что каждый ряд мог быть использован для представления чисел от 0 до 3 × 5 + 4 × 1 = 19. Использование 13 рядов позволяло набрать числа вплоть до 2013 – 1, что составляет более 80 квадриллионов, то есть примерно в сто раз больше, чем число песчинок, которые потребуются, чтобы выложить расстояние от Земли до Солнца.

Количество бусин в одном непоуальцинцине (13 × 7 = 91) приблизительно соответствует количеству дней каждого из времён года, в двух непоуальцинцинах (91 × 2 = = 182) — количеству дней от посева кукурузы до её сбора, в трёх (91 × 3 = 273) — средней продолжительности беременности у людей в днях, в четырёх (91 × 4 = 364) — продолжительности года в днях с ошибкой всего-то примерно в 1,25 дня[23].

Проблема с непоуальцинцином только одна — весьма вероятно, что он вовсе никогда не существовал. По сути, все современные источники отталкиваются от исследований мексиканского инженера-строителя Давида Эспарца Идальго. По словам исследователя, переоткрытие непоуальцинцина стоило ему развода и 18 лет скитаний по горам, пустыням и джунглям[24]. Идальго написал несколько книг про непоуальцинцин и активно пропагандировал использование этого устройства в педагогических целях, однако научное сообщество относится к его выводам довольно прохладно, так как материальная база исследований Идальго более чем скудна.

Немного лучше дела обстоят с абаком инков — «юпаной» (yupay на языке кечуа означает «счёт»). Слово «юпана» на самом деле используется для обозначения двух разных типов объектов. Дощечка-юпана, или археологическая юпана, — дощечка или плитка, на одной из сторон которой вырезана система лотков различного размера. Предполагается, что вычисления производились при помощи зёрен или камешков, размещаемых в лотках. Первая из таких дощечек была найдена в районе города Куэнка в Эквадоре в 1869 г. С тех пор подобные объекты попадались археологам не единожды — они выполнены из различных материалов и довольно сильно отличаются друг от друга.

Также известна так называемая юпана Пома де Айяла — изображение на 360-й странице иллюстрированного манускрипта «Первая новая хроника и доброе правление» (El primer nueva corónica y buen gobierno), созданного в конце XVI — начале XVII в. Отдельный интересный вопрос: какова степень участия в её создании формального автора этой хроники Фелипе Гуамана Пома де Айяла, представителя знатного рода Южного Перу, служившего переводчиком у испанцев? Юпана из хроники представляет собой клетчатое поле размером 5 × 4 клетки. В клетках изображены маленькие окружности, некоторые из них закрашены. Рядом с полем нарисован человек, держащий в руках кипу (от khipu — «узел» на языке кечуа) — сплетение верёвочек с узелками. Сопроводительный текст на следующей странице сообщает примерно следующее: «Они производили счёт на счётной доске, ведя его так: сто тысяч, десять тысяч, [одна тысяча], сто, десять, доходя до единицы. Всё то, что происходит в этом королевстве, они фиксируют: и праздники, и воскресенья, и месяцы, и годы. И каждый город, и селение, и посёлок имели из числа индейцев этих означенных счётчиков и казначеев этого королевства, и считали они следующим образом…» Далее перечисляются названия цифр и чисел на кечуа[25].

Рис. 10. Юпана Пома де Айяла

Хотя юпана Пома де Айяла и напоминает археологические юпаны, нельзя обойти стороной и разницу. В первую очередь в глаза бросается то, что, в отличие от прямоугольных полей на изображении, лотки археологических юпан часто другой формы.

Существует несколько интерпретаций изображения хроники Пома де Айяла. Например, в 2008 г. Чинция Флорио предположила, что закрашенные кружки соответствуют единицам, пустые — десяткам, а на юпане изображена операция 32 × 5 = 32 × (2 + 3) = (32 × 2) + (32 × 3) = = 64 + 96 = 160, но результатом стало число 151, потому что автор хроники перепутал цвет одного из кружков[26].

«Первая новая хроника и доброе правление» — не единственный источник о способах счёта инков. Хосе де Акоста — испанский историк, географ и натуралист, миссионер и член ордена иезуитов — в трактате «Естественная и нравственная история Индии» (Historia natural y moral de las Indias) пишет следующее: «они берут зёрна [кукурузы] и кладут одно сюда, три туда, восемь из другой части; они вынимают из коробки и заменяют три других зёрнышка одни на другие, чтобы в итоге получить безошибочный результат».

В общем, юпана выглядит в качестве потенциального аналога абака более солидно, чем непоуальцинцин, но и тут есть над чем поломать голову будущим классикам абакологии.

Китайский абак называется «суаньпань» (кит. трад. 算盤, упр. 算盘, пиньинь: suànpán), буквально: «счётная доска». В древнекитайском трактате под названием «Шу шу цзи и» (数术记遗), название которого можно перевести как «Заметки для потомков об искусстве чисел» или «Мемуары о правилах счёта», впервые упоминается «чжу суань» (珠算) («вычисление при помощи бусин»). Предполагается, что автором этого трактата является древнекитайский астроном, математик и философ Сюй Юэ. Историки считают, что указание на подобный способ счёта означает наличие инструмента, подобного суаньпаню[27], но достоверные изображения древнекитайского абака появляются только в начале XII в.[28] Суаньпань — это прямоугольная рамка, в которой находится девять или более параллельных друг другу спиц или верёвок. Перпендикулярно им суаньпань разделяется на две неравные части дополнительной планкой. В большом отделении («земля») на каждой спице нанизано по пять бусин, в меньшем («небо») — по две. В основе суаньпаня лежит десятичная система счисления. Бусины, находящиеся «в небе», означают пятёрки, а «на земле» — единицы. Крайние бусины могут применяться для выполнения действий, связанных с переносом разряда, а также позволяют при необходимости производить расчёты в шестнадцатых долях, необходимые в классической китайской системе измерения весов[29].

Рис. 11. Китайский абак «суаньпань»

Помимо суаньпаня, китайская традиция счёта знает и более древний инструмент — счётные палочки, несколько найденных комплектов которых датируются III в. до н. э. Впрочем, существуют весьма убедительные свидетельства того, что счётные палочки применялись и раньше. Например, древнекитайский трактат «Дао дэ цзин» (кит. трад. 道德經, упр. 道德经, пиньинь: Dàodéjīng), традиционно датируемый VI в. до н. э. и созданный, по преданию, легендарным философом Лао-цзы, содержит высказывание: «Тот, кто хорош в счёте, не использует счётных палочек»[30].

В XIV в. китайский суаньпань был завезён в Японию, где лишился обеих «лишних» косточек «в небе» и «на земле» и стал традиционным японским соробаном (算盤 / そろばん)[31].

Рис. 12. Японский соробан

Примерно в то же время (около 1400 г.) китайский абак попадает в Корею. Корейцы называют его «чу пхан» (주판), «су пхан» (수판) или «чу сан» (주산).

«Абхидхармакоша» (санскр. अभिधर्मकोश abhidharmakośa — дословно «корзина абхидхармы») — сочинение в стихах, написанное буддийским философом Васубандху в IV в. н. э., недвусмысленно свидетельствует о том, что автору было известно устройство, похожее на абак. Васубандху, цитируя рассуждения проповедника и философа Васумитры о дхарме, функционирующей в разных временных модусах, пишет буквально следующее: «Это подобно тому, как шарик (костяшка), передвинутый в позицию единиц, называется единицей, в позицию сотен — сотней, в позицию тысяч — тысячей»[32].

Русские счёты являются, по всей видимости, довольно поздним устройством, по поводу происхождения которого тем не менее нет окончательной ясности. В 1664–1665 гг. в составе голландского посольства Якоба Борейля Россию посетил Николаас Витсен, голландский политик, предприниматель, картограф и будущий бургомистр Амстердама. В своём путешествии Витсен вёл дневник, делал многочисленные заметки и зарисовки. В 1692 г. он выпустил в Амстердаме сочинение «Северная и Восточная Тартария» (Noord en Oost Tartarye), в котором мы находим следующее суждение: «Этот старый Строганов привёз в Россию, как говорят, счёты, или арифметику, которые они ещё употребляют до сего дня. Это костяные бусинки, нанизанные на железные прутики»[33]. Этот короткий фрагмент текста цитируют позже Миллер в своём «Описании Сибирского царства»[34], а вслед за ним и Карамзин[35] в «Истории государства Российского». Хотя ни Карамзин, ни Миллер, ни тем более Витсен напрямую не называют счёты непосредственным наследником китайского суаньпаня, идея заимствования именно китайского абака через татар является заманчивой. Но всё-таки вряд ли стоит выстраивать теорию на основе одного-единственного исторического анекдота[36] и частичного конструктивного сходства двух устройств. Тем более что счёты всё-таки заметно отличаются от суаньпаня — вертикальной ориентацией, отсутствием разделителя, иным способом набора чисел. Сам термин «счёты» в варианте «счоты» впервые встречается в «Переписной книге домовой казны патриарха Никона», составленной в 1658 г.: «Да в коробе ево ж Сергиева рухлядь:

Схима.

Два свешника, один медной, а другой железной полужен.

Вески да два фунта.

Зеркало в досках.

Счоты.

Два ножика, у одного черен репчатой жуки серебряные, а у другова

черен костяной рыбей» и так далее[37].

К XVI–XVII вв. относятся русские рукописные арифметики, объединённые общим названием «Цифирная счётная мудрость». В более ранних списках описываются «дощаный счёт» и «счётная дщица». По всей видимости, именно эти приспособления являются предшественниками счётов.

Хотя в наши дни счёты уже практически вышли из обихода, они оставили множество следов в русском языке. Именно им мы обязаны такими словами и выражениями, как «скостить», «скинуть», «накинуть», «сбрасывать со счетов», «сводить счёты» и тому подобное.

Использованию счётов и дощаного счёта предшествовал «счёт костьми», при котором счётные косточки раскладывались на столе[38]. Подобный способ был, по всей видимости, универсален для Древнего мира. Например, о подсчёте при помощи гальки (λογίδονται ψήφοισι)[39] в Древнем Египте мы знаем от Геродота, отмечавшего, что египтяне выкладывали камешки справа налево, в направлении противоположном принятому у греков[40], при этом само слово «абак» Геродот в данном контексте не упоминает, и достоверные древнеегипетские изображения абака нам неизвестны[41]. Точно так же герой «Агамемнона» Эсхила упоминает о подсчёте убитых при помощи камешков (τί τοὺς ἀναλωθέντας ἐν ψήφῳ λέγειν — «Почему мы должны камешками подсчитывать убитых?»)[42]. Дважды подобный способ счёта встречается у Аристофана в комедии «Осы». Первый раз Филоклеон просит Зевса превратить его в один из камней, на которых ведут подсчёт голосов (ἢ δῆτα λίθον με ποίησον ἐφ᾽ οὗ / τὰς χοιρίνας ἀριθμοῦσι)[43]. Эта цитата интересна тем, что здесь упоминаются не камешки, при помощи которых осуществляется счёт, а камень, на поверхности которого данные расчёты производятся. Во второй раз Бделиклеон говорит отцу, что доходы и расходы (в их конкретном случае) можно счесть на пальцах, не прибегая к камешкам (καὶ πρῶτον μὲν λόγισαι φαύλως, μὴ ψήφοις ἀλλ᾽ ἀπὸ χειρός, / τὸν φόρον…)[44].

В «Афинской политии», написанной Аристотелем или одним из его учеников, описывается процедура судебного голосования при помощи абака (ἐξερῶσι ἐπὶ ἄβακα τρυπήματα ἔχοντα ὅσαιπερ εἰσὶν αἱ ψῆφοι) с отверстиями для камешков, каждый из которых соответствовал одному поданному голосу[45].

Первые археологические свидетельства использования абака в Древней Греции относятся к V в. до н. э.[46] Наверное, наиболее известное из них — изображение на «Вазе Дария» (340–320 гг. до н. э.), хранящейся в настоящее время в Национальном археологическом музее Неаполя[47]. На сцене, изображающей военный совет, мы видим человека, сидящего за небольшим столиком, на поверхности которого начертаны буквы и разложены камешки.

Рис. 13. Военный совет Дария. Изображение на «Вазе Дария» (340–320 гг. до н. э.)

Абак в своих сочинениях упоминают Демосфен и Полибий[48]. Последний пишет: «Придворные — как камни на счётной доске: захочет счётчик, и они будут стоить один халк, а захочет — так и целый талант»[49]. Похожую мысль Диоген Лаэртский приписывает Солону[50].

Абак, найденный на греческом острове Саламин в 1846 г. (саламинская доска), относится к 300 г. до н. э., что делает его древнейшей счётной доской, обнаруженной до сих пор. Это плита белого мрамора размером 149 × 75 × 4,5 см с нанесёнными на неё метками для счёта[51].

Рис. 14. Саламинская доска (300 г. до н. э.)

  1. ↑ Boyer C. B., Merzbach U. C. (2011). A History of Mathematics. John Wiley & Sons // https://www.google.ru/books?id=bR9HAAAAQBAJ
  2. ↑ Википедия // https://ru.wikipedia.org/wiki/Абак (версия от 11.03.2018).
  3. ↑ См., напр.: Большой энциклопедический словарь (2002) / 2-е изд., перераб. и доп., с ил. // https://dic.academic.ru/dic.nsf/enc3p/44770
  4. ↑ Donnegan J. Patton R. B. (1838). A New Greek and English Lexicon: Principally on the Plan of the Greek and German Lexicon of Schneider: the Words Alphabetically Arranged. Hilliard, Gray & Company.
  5. ↑ Шанский Н. М., Боброва Т. А. (2004) Школьный этимологический словарь русского языка. Происхождение слов. — М.: Дрофа.
  6. ↑ A Greek-English lexicon to the New Testament by Greenfield, William, 1799-1831; Green, Thomas Sheldon, 1803 or 1804-1876; Hastings H. L. (Horace Lorenzo), 1831-1899; Stearns, Wallace N. (Wallace Nelson), 1866-; Thayer, Joseph Henry, 1828-1901 // https://www.gutenberg.org/files/40935/40935-h/40935-h.htm
  7. ↑ Михельсон А. Д. (1865) Объяснение 25000 иностранных слов, вошедших в употребление в русский язык, с означением их корней.
  8. ↑ A Dictionary of Greek and Roman Antiquities (1890) William Smith, LLD, William Wayte, G. E. Marindin, Ed // http://www.perseus.tufts.edu/hopper/text?doc=Perseus%3Atext%3A1999.04.0063%3Aalphabetic+letter%3DA%3Aentry+group%3D1%3Aentry%3Dabacus-cn
  9. ↑ Online etymology dictionary © 2001-2018 Douglas Harper. All rights reserved // https://www.etymonline.com/word/abacus
  10. ↑ Huehnergard J. (2011). "Appendix of Semitic Roots, under the root ʾbq.". American Heritage Dictionary of the English Language (5th ed.). Houghton Mifflin Harcourt Trade.
  11. ↑ Online etymology dictionary © 2001-2018 Douglas Harper. All rights reserved // https://www.etymonline.com/word/abacus
  12. ↑ Robertson J. (2019). Robertson's Words for a Modern Age: A Dictionary of English Vocabulary Words Derived Primarily from Latin and Greek Sources, Presented Individually and in Family Units // https://wordinfo.info/
  13. ↑ Ifrah G. (2001). The Universal History of Computing: From the Abacus to the Quantum Computer. New York, NY: John Wiley & Sons, Inc., р. 11.
  14. ↑ Ifrah G. (2000). The Universal History of Numbers: From prehistory to the invention of the computer., John Wiley and Sons. Translated from the French by David Bellos, E. F. Harding, Sophie Wood and Ian Monk.
  15. ↑ Macey S. L. (1989). The Dynamics of Progress: Time, Method, and Measure, Atlanta, Georgia: University of Georgia Press, p. 92.
  16. ↑ Ndimele O., Chan S.(2016). The Numeral Systems of Nigerian Languages. Oxford: African Books Collective. Retrieved June 21, 2018, from Project MUSE database.
  17. ↑ Francis W. (1988). Gazetteer of South India. Mittal Publ.
  18. ↑ Caughley R. C. (1989). Chepang — a Sino-Tibetan language with a duodecimal numeral base?, in D. Bradley et al. (eds.).
  19. ↑ de Buffon G. L. L., C'epède L. (1839). Oeuvres complètes de Buffon. Rapet et cie.
  20. ↑ Foundation and First Generation // http://www.dozenal.org/drupal/content/foundation-and-first-generation.html
  21. ↑ The Dozenal Society of Great Britain // http://www.dozenalsociety.org.uk/
  22. ↑ Karttunen F. E. (1992). An Analytical Dictionary of Nahuatl. University of Oklahoma Press // https://books.google.ru/books?id=s4LURGT0h2AC
  23. ↑ Kane N. (2016). Maya Math Simplified. Spangenhelm Publishing // https://books.google.ru/books?id=8vN6DQAAQBAJ
  24. ↑ Ancient Aztec 'Computer' beats electronic brains / Radford Journal Weekly (November 3, 1977) // https://newspaperarchive.com/radford-journal-weekly-nov-03-1977-p-2/
  25. ↑ Гуаман Пома де Айяла Ф. (2011) Первая новая хроника и доброе правление (доколумбовый период) / Пер. со староисп. В.А. Кузьмищева; отв. ред. Н.Ю. Кудеярова. — М.: Памятники исторической мысли // http://www.piminfo.ru/catfile/bbook_Pdf_small_275.pdf
  26. ↑ Florio C. Risposta aperta a Subhash Kak sulla decifrazione della yupana di Guaman Poma // https://www.academia.edu/6343696/Risposta_aperta_a_Subhash_Kak_sulla_yupana_di_Guaman_Poma_de_Ayala
  27. ↑ Volkov A. K. (1994). Large Numbers and Counting Rods / Extrême-Orient, Extrême-Occident, 1994, n°16. Sous les nombres, le monde: Matériaux pour l'histoire culturelle du nombre en Chine ancienne, pp. 71—92 // https://doi.org/10.3406/oroc.1994.991
  28. ↑ Igarashi Y., Altman T., Funada M., Kamiyama B. (2014). Computing: A Historical and Technical Perspective. CRC Press // https://books.google.ru/books?id=eabNBQAAQBAJ
  29. ↑ Moon P. H. (1971). The abacus: its history, its design, its possibilities in the modern world. Gordon and Breach Science Publishers // https://books.google.ru/books?id=G1LxAAAAMAAJ
  30. ↑ Wagner R. G., Wang B. (2003). A Chinese Reading of the Daodejing: Wang Bi's Commentary on the Laozi with Critical Text and Translation. State University of New York Press // https://books.google.ru/books?id=bUZNAAAAQBAJ
  31. ↑ Gullberg J., Hilton P., Gullberg P. (1997). Mathematics: From the Birth of Numbers. W. W. Norton // https://books.google.ru/books?id=E09fBi9StpQC
  32. ↑ Васубандху (2006). Энциклопедия буддийской канонической философии (Абхидхармакоша) / Составление, перевод, комментарии, исследования Е. П. Островской, В. И. Рудого. — СПб.: Изд-во С.-Петерб. ун-та. С. 74 // http://abhidharma.ru/A/Guru%20Mahasiddhi/Content/Vasubandhu/Abhidharmakosha%20O.R.%20V-VI.pdf
  33. ↑ Витсен Н. (2010). Северная и Восточная Тартария: в 3 т. — Амстердам: Pegasus. 624; 608; 584 с // https://www.pegasusboek.nl/severnaia-i-vostotsnaja-tartarija.html
  34. ↑ Миллер Г. Ф. (1937). История Сибири. — М.: Издательство АН СССР. 637 с, 2 карты // https://www.runivers.ru/upload/iblock/2f8/miller%201.pdf
  35. ↑ Карамзин Н. М. История государства Российского // http://www.kulichki.com/inkwell/text/special/history/karamzin/kar09_06.htm
  36. ↑ * Соседствующего, между прочим, с историей о происхождении фамилии Строганов от умерщвления основателя рода татарами, выполненного путём строгания, то есть изрубливания на мелкие кусочки.
  37. ↑ Цепков А. И. (сост.). Сочинения Григория Скибинского. Переписная книга домовой казны патриарха Никона. — Рязань: Александрия. С. 463 // https://mirlib.ru/knigi/history/212098-sochineniya-grigoriya-skibinskogo-perepisnaya-kniga-domovoy-kazny-patriarha-nikona.html
  38. ↑ Спасский И. Г. (1952). Происхождение и история русских счётов // Историко-математические исследования. — М.: ГИТТЛ. № 5. С. 269—420 // http://pyrkov-professor.ru/default.aspx?tabid=195&ArticleId=43
  39. ↑ The History Of Herodotus. Vol. 1 (of 2). Translator: G. C. Macaulay // https://www.gutenberg.org/files/2707/2707-h/2707-h.htm
  40. ↑ Smith D. E. (1958). History of Mathematics. Dover Books on Mathematics. 2: Special Topics of Elementary Mathematics. Courier Dover Publications.
  41. ↑ Smith D. E. (1958). History of Mathematics. Dover Books on Mathematics. 2: Special Topics of Elementary Mathematics. Courier Dover Publications.
  42. ↑ Aeschylus, Agamemnon (Greek) (ed. Herbert Weir Smyth, Ph. D.) // http://data.perseus.org/citations/urn:cts:greekLit:tlg0085.tlg005.perseus-grc1:538-582
  43. ↑ Aristophanes. Aristophanes Comoediae, ed. F. W. Hall and W. M. Geldart, vol. 1. F. W. Hall and W. M. Geldart. Oxford. Clarendon Press, Oxford. 1907 // http://data.perseus.org/citations/urn:cts:greekLit:tlg0019.tlg004.perseus-grc1:316-333
  44. ↑ Aristophanes. Aristophanes Comoediae, ed. F. W. Hall and W. M. Geldart, vol. 1. F. W. Hall and W. M. Geldart. Oxford. Clarendon Press, Oxford. 1907 // http://data.perseus.org/citations/urn:cts:greekLit:tlg0019.tlg004.perseus-grc1:650-695
  45. ↑ Athenaion Politeia, ed. Kenyon. Oxford. 1920 // http://data.perseus.org/citations/urn:cts:greekLit:tlg0086.tlg003.perseus-eng1:69.1
  46. ↑ Ifrah G. (2001). The Universal History of Computing: From the Abacus to the Quantum Computer. New York, NY: John Wiley & Sons, Inc.
  47. ↑ Trendall & Cambitoglou 1982 p. 495, no. 18/38, pl. 176,1; FR pl. 88 // http://www.perseus.tufts.edu/hopper/artifact?name=Naples+3253&object=vase
  48. ↑ Pullan J. M. (1968). The History of the Abacus. New York, NY: Frederick A. Praeger, Inc., Publishers.
  49. ↑ Historiae. Polybius. Theodorus Büttner-Wobst after L. Dindorf. Leipzig. Teubner. 1893 // http://www.perseus.tufts.edu/hopper/text?doc=urn:cts:greekLit:tlg0543.tlg001.perseus-eng1:5.26
  50. ↑ Diogenes Laertius, Lives of Eminent Philosophers R. D. Hicks, Ed. (1972) // http://www.perseus.tufts.edu/hopper/text?doc=urn:cts:greekLit:tlg0004.tlg001.perseus-eng1:1.2
  51. ↑ Williams M. R. (1997). Baltes, Cheryl, ed. A History of Computing technology (2nd ed.). Los Alamitos, CA: IEEE Computer Society Press.

‎

Loading comments...
Источник — http://wiki.markoff.science/index.php?title=2.1.1_Счёты,_абак_и_астролябия&oldid=1085