2.4.1 Юность Бэббиджа. Проект де Прони как источник вдохновения

Чарльз Бэббидж родился в Лондоне в 1791 г. в семье банкира Бенджамина Бэббиджа и его жены Элизабет Бэббидж (Тип). Два маленьких брата Бэббиджа, родившиеся в 1794 и 1796 гг., умерли во младенчестве, и только сестра, Мэри Энн, родившаяся в 1798 г., выжила и даже смогла пережить Чарльза. Своё образование Бэббидж начал в возрасте восьми лет в частной школе в Альфингтоне, однако здоровье мальчика было слабым, и учебную нагрузку старались ограничивать. После начальной школы Чарльз поступает в среднюю школу преподобного Стивена Фримена, также известную под названием «Холмвуд» или «Академия Холмвуда». Это было небольшое учебное заведение на 30 учеников, расположенное в красном кирпичном здании в верхней части Бейкер-стрит в Энфилде (не путать с одноимённой улицей в районе Мэрилебон, на которой сэр Артур Конан Дойл разместил обиталище Шерлока Холмса).

Найденная в школьной библиотеке книга Джона Уорда «Путеводитель молодого математика» (Ward’s Young Mathematician’s Guide) произвела особенно сильное впечатление на юного Бэббиджа. Его интерес к математике был очевиден и зашёл так далеко, что вместе с одним из однокашников Чарльз занимался ею самостоятельно перед началом школьных уроков. Позднее он продолжил занятия под руководством священника-тьютора недалеко от Кембриджа. Эти занятия продолжались в течение нескольких лет, и, наконец, перед поступлением в Кембриджский университет Бэббидж провёл некоторое время в Тотнесе, где занимался классическими языками под руководством оксфордского наставника. Будучи страстно увлечённым алгеброй, он проводил досуг, изучая все математические работы, которые попадали в его руки. К тому времени, когда Чарльз отправился в Кембридж, он уже был вполне сформировавшимся математиком, знакомым с «Принципами аналитических вычислений» Роберта Вудхауза, «Теорией аналитических функций» Жозефа Луи Лагранжа, «Основами анализа» Марии Гаэтаны Аньези и другими работами по исчислению «флюксий» (устаревшее название производных).

В апреле 1810 г. Бэббидж поступает в кембриджский Тринити-колледж, а спустя два года переходит в колледж Питерхаус. Здесь он активно включается в полную энергией студенческую жизнь: играет в шахматы, участвует в ночных шестипенсовых играх в вист, периодически пропускает лекции и церковные службы ради прогулок по реке с друзьями. В Кембридже Бэббидж знакомится с сыном знаменитого астронома Уильяма Гершеля Джоном, который поступил в Колледж Святого Иоанна в 1809 г., и вскоре они становятся близкими друзьями. Бэббидж придерживался радикальных взглядов: он восхищался наполеоновской Францией (с которой Британия находилась в состоянии войны), осуждал догматизм, проявлявшийся в подчинении университетской жизни религиозным принципам, сетовал на отсутствие восприимчивости к континентальным теориям в области математики. Чарльза расстраивало, что университетская программа мало прибавляет к имевшимся у него знаниям в области математики, поэтому в своём образовании он больше опирался на программу самостоятельного обучения, основой которой стало изучение трудов иностранных математиков.

Вместе с Джоном Гершелем и Джорджем Пикоком (в будущем — известным математиком) Бэббидж переводит на английский язык «Трактат по дифференциальному и интегральному исчислению» (Traité du calcul différentiel et intégral) Сильвестра Лакруа и отстаивает превосходство нотации дифференцирования Лейбница ($\frac{dx}{dt}$) перед ньютоновской ($\dot{x}$), в то время считавшейся в Англии своеобразной научной святыней.

Бэббидж был звездой Питерхауса, однако в 1814 г. получил диплом бакалавра без отличия (Poll degree), а в 1817-м — степень магистра искусств (Master of Arts): в ходе публичных диспутов, являвшихся частью предварительного отбора для получения диплома с отличием, Бэббидж отстаивал утверждение о том, что бог является материальным агентом. Ведущий диспута преподобный Томас Джефсон объявил это суждение богохульным и отверг кандидатуру Бэббиджа. Не до конца ясно, был ли в результате Бэббидж не допущен к экзамену на степень с отличием или же сам не захотел принимать в нём участие, однако считается, что именно этот эпизод привёл Чарльза к разочарованию в кембриджском сообществе и уходу из университета. Впрочем, позже Бэббидж с теплотой вспоминал годы, проведённые в Кембридже.

Трагикомической подробностью биографии обидчика Бэббиджа стало то, что в 1823 г. святоша предстал перед судом по обвинению в содомии, и лишь высокий социальный статус позволил ему избежать сурового наказания^, .

В 1816 г. Бэббидж был избран членом Лондонского королевского общества, а в 1820‑м — членом Королевского общества Эдинбурга. Он участвовал в создании Королевского астрономического общества в 1820 г. и занимал посты секретаря (1820–1824), а затем — вице-президента, иностранного секретаря и члена совета. Немногое известно о семейной жизни Бэббиджа. Он женился на Джорджине Уитмор в 1814 г., и у них было восемь детей, четверо из которых умерли в детстве. 1827 год стал трагическим годом для Бэббиджа: он потерял отца, жену и двоих детей, его собственное здоровье было серьёзно подорвано. После смерти Джорджины Бэббидж более не вступал в брак.

В 1819 г. Бэббидж впервые посетил Париж, где познакомился с несколькими ведущими членами Французской академии наук, в том числе с математиками Пьером-Симоном Лапласом и Жозефом Фурье, с которыми его связала крепкая дружба. По всей видимости, именно во время этого визита Бэббидж узнал о великом французском проекте по созданию логарифмических и тригонометрических таблиц, организованном бароном Гаспаром де Прони, и именно этот проект вдохновил Бэббиджа на дело всей его жизни.

Де Прони начал свой проект в 1790 г., вскоре после Французской революции. Новое правительство планировало реформировать многие из древних институтов Франции и, в частности, создать справедливую систему налогообложения имущества. Для этого были необходимы современные карты Франции, создание которых было поручено де Прони, назначенному главой Кадастрового бюро Франции. Его задача была усложнена тем, что правительство одновременно решило заменить старую королевскую систему мер и весов путём введения новой метрической системы. Это потребовало от Бюро создания полного набора тригонометрических и логарифмических таблиц для французского кадастра. На тот момент это был самый крупный проект по изготовлению таблиц, который когда-либо знал мир, и де Прони решил положить в его основу принципы фабричного производства. Он принял за основу самый известный экономический текст своего времени — «Богатство народов» Адама Смита, опубликованный в 1776 г. В нём Смит отстаивал принцип разделения труда, который проиллюстрировал на примере производства булавок. Смит демонстрировал, что создание булавки можно разделить на несколько отдельных операций: нарезку проволоки на части, формирование головки булавки, заточку, полировку, упаковку и так далее. Специализация каждого работника на какой-либо одной операции приводила к росту производительности труда по сравнению с ситуацией, когда один человек выполнял все операции сразу.

Де Прони решил применить тот же метод в стоящей перед ним задаче — то есть в некотором смысле организовать производство логарифмов на тех же принципах, на которых было основано производство булавок. Де Прони разделил свою «фабрику по производству таблиц» на три отдела: первый состоял из нескольких выдающихся математиков, в число которых входили Адриен Мари Лежандр и Лазар Карно. В задачи этого отдела входил выбор математических формул для расчётов. Им подчинялся небольшой второй отдел, включавший контролёров, своеобразных «менеджеров среднего звена», которые организовали вычисления и занимались сведением результатов, подготавливая их к печати. ​И наконец, третий и самый большой отдел состоял из 60–80 людей-вычислителей. Вычислители использовали в своей работе «метод разделённых разностей», основанный на выполнении всего лишь двух основных операций: сложения и вычитания, что не требовало от них ни специальных математических знаний, ни высокой квалификации. По большей мере вычислители были бывшими парикмахерами, потерявшими работу из-за того, что причёски аристократии стали одним из самых ненавистных символов старого режима.

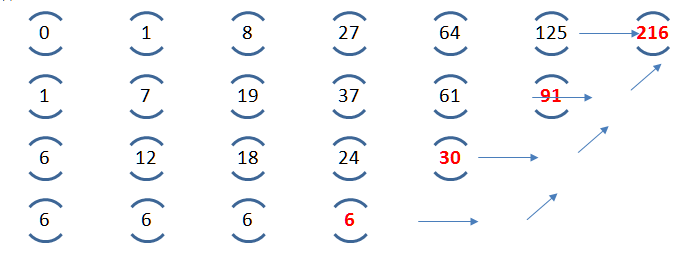
Понять принцип метода разделённых разностей несложно, это вам не бином Ньютона… Хотя подождите, упс… На самом деле это он самый и есть, а точнее — это метод, при помощи которого можно находить коэффициенты ньютоновского интерполяционного полинома. Как самостоятельный подход метод разностей оформился в работах Брука Тейлора, но в его основе лежали ранее известные закономерности. Мы, впрочем, не будем здесь погружаться в пучины математики и даже спорить о том, кому в данном случае принадлежит приоритет в изобретении этого метода — Бруку Тейлору, Исааку Ньютону или Блезу Паскалю. Ограничимся небольшим примером. Предположим, что мы хотим рассчитать последовательные значения функции y = x³. Давайте посмотрим, как начинается этот ряд: при x, начинающемся с нуля, y принимает последовательно следующие значения: 0³ = 0, 1³ = 1, 2³ = = 8, 3³ = 27, 4³ = 64, 5³ = 125 и так далее.

Теперь посчитаем разности между соседними числами в этой последовательности (так называемые разности первого порядка).

Теперь по аналогии рассчитаем разности второго порядка, находя разности между соседними числами в полученной нами на прошлом шаге последовательности разностей первого порядка.

Теперь вычислим разности третьего порядка.

Мы видим, что разности третьего порядка постоянны. Как бы долго мы ни продолжали исходную последовательность, в данном случае разности третьего порядка будут неизменно представлять собой шестёрки. Если бы исходный многочлен имел степень 4, например y = x⁴ или y = 2x⁴ + 3x² + 5x + 1, то нам пришлось бы использовать уже четыре порядка разностей, и в четвёртом порядке мы снова получили бы неизменные значения. Используя эту закономерность, несложно теперь продолжить исходную последовательность. Поскольку четвёртой разностью третьего порядка у нас будет всё та же шестёрка, мы можем вычислить пятую разность второго порядка: 24 + 6 = 30. Теперь шестую разность первого порядка: 61 + 30 = 91 и, наконец, седьмой элемент исходной последовательности: 125 + 91 = 216. И действительно, 6³ = 216.

Расчёты в рамках проекта де Прони заняли около десятилетия, в 1801 г. таблицы были готовы к печати, однако их изданию помешала череда финансовых и политических кризисов, в которую погрузилась Франция начала XIX в. Необходимая для печати сумма средств так никогда и не была найдена, и единственным результатом проекта, доступным Бэббиджу в 1819 г., стала рукописная версия таблиц, хранившаяся в библиотеке Французской академии наук.

‎

Loading comments...