3.2 Крестики-нолики

Есть и такая, где каждый выводит по трое шашек,

А побеждает, кто смог в линию выстроить их.

Много есть игр, и надо их знать красавице умной,

Надо играть: за игрой часто родится любовь.

Овидий Публий Назон. Наука любви

Несмотря на исключительную математическую простоту нима, эта игра всё-таки не слишком популярна. Если вы попросите случайного человека назвать вам самую простую настольную игру, то, скорее всего, первой игрой, которая придёт ему в голову, будут крестики-нолики.

Из популярных источников^, можно узнать, что ранний вариант этой игры, носивший название «по три камешка» (Terni lapilli), был распространён в Древнем Риме примерно с I в. до н. э. Начало старинной игры ничем не отличалось от современного варианта: игроки последовательно выставляли свои фишки на поле размером 3 × 3 (при этом первый ход в центр поля был запрещён), а если кому-то из них удавалось выстроить их в ряд, то он выигрывал партию. Однако после того, как три фишки каждого цвета были выставлены на доску, начинался второй этап игры, в ходе которого игроки могли поочерёдно перемещать одну из своих фишек на любое незанятое соседнее поле, при этом критерий выигрыша оставался неизменным — нужно было построить три фишки в ряд. Размеченные поля для игры (их называли tabula lusoria — доска для игры) встречаются на всей бывшей территории Римской империи.

Крестики-нолики… Казалось бы, что может быть проще? Но если задаться вопросом, откуда взялась эта игра, то можно нечаянно открыть портал в другие миры.

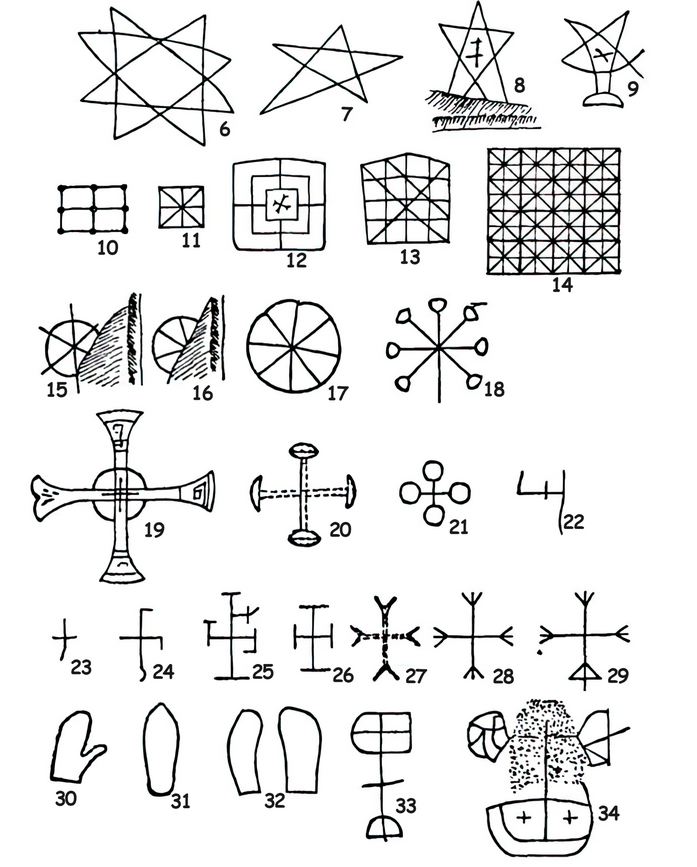
Например, в английской «Википедии» написано, что игра появилась в Древнем Египте, называются даже примерные даты: «Игры на полях типа „три-в-ряд“ могут быть отслежены вплоть до Древнего Египта, где поля для таких игр были обнаружены на черепице (?), датированной примерно 1300 годом до н. э.». При этом в качестве источника приводится ссылка на пару научно-популярных книг. Причём источники отчасти лишь добавляют путаницы, потому что в книге Марлы Паркер говорится о том, что поля для игры найдены на черепице древнеегипетского храма, построенного 3300 лет назад, в то время как в книге Клавдии Заславски говорится уже о плитах из песчаника. Но чёрт с ним, будем считать, что плиты из песчаника — это такая суровая челябинская древнеегипетская черепица, главное, Заславски называет сам храм — Поминальный храм Се́ти I, который посвящён второму фараону XIX династии, отцу Рамсеса II. Храм расположен в Фиванском некрополе в Верхнем Египте, через реку напротив Луксора, возле деревни Курна. Древнеегипетское название этого храма — Великий храм Мен-Маат-Ра Сети в доме Амона в западной части Фив. Кроме того, Заславски сообщает, что открытие было сделано более ста лет назад при изучении учёными потолка храма. Эта информация позволяет отследить источник сведений вплоть до книги британского инженера Генри Паркера, впервые вышедшей в свет в 1909 г. Сама книга посвящена, впрочем, вовсе не Египту, а истории Цейлона (ныне — Шри-Ланки). В книге Паркер приводит 34 пиктограммы, обнаруженные на крыше храма в Курне. Он приходит к выводу, что три из них были нанесены на плиту до того, как она стала частью строения, поскольку они обрываются на краях плиты, что, по мнению Паркера, означает, что плита была укорочена во время строительства и вместе с отпиленной частью были удалены края изображений. Также Паркер считает весьма вероятным, что оставшаяся 31 пиктограмма тоже была нанесена на плиту строителями храма. Паркер предполагает, что одна из пиктограмм (судя по описанию — № 10) является полем для игры, подобной современным крестикам-ноликам.

Рис. 53. Пиктограммы, обнаруженные на крыше храма в Курне

Является ли гипотеза Паркера, содержащая целый ряд допущений, достаточным основанием для того, чтобы считать, что древние египтяне знали игру, похожую на крестики-нолики, особенно учитывая то, что египтологам до сих пор не удалось отыскать ни одного упоминания этой игры или хотя бы изображения, подобного указанному Паркером?.. Отмечу, что о древнеегипетских настольных играх мы знаем не так уж мало. Например, «древнеегипетские шахматы» (сенет) встречаются и на изображениях в гробницах и удостоены упоминания в древнеегипетских текстах; более того, до нас даже дошло несколько древних комплектов для игры в сенет.

Гипотеза Паркера перекочевала затем в книгу Харольда Мюррея, посвящённую исследованию истории настольных игр (в своей книге Мюррей приводит 7 из 34 пиктограмм из книги Паркера), а затем в работы Роберта Белла, признанного специалиста в этой области, откуда уже, по всей видимости, проникла в качестве установленной истины в научно-популярные книги, а оттуда — в «Википедию».

В наши дни предположение Паркера о том, что все пиктограммы, найденные на крыше храма в Курне, были нанесены на неё до его постройки, подвергается серьёзному сомнению: как минимум часть символов имеет коптское происхождение, поэтому датировка пиктограмм сегодня представляется неопределённой. Египет в разное время находился под властью персов, греков, римлян, византийцев, арабов, и определить точно, к какой эпохе относятся граффити, сегодня вряд ли возможно.

В 1990-е гг. исследовательская группа GERSAR (Groupe d’Études, de Recherches et de Sauvegarde de l’Art Rupestre, Группа изучения, исследования и защиты наскального искусства) под руководством доктора Кристиана Вагнёра составила каталог из более чем тысячи изображений, напоминающих поля для игр типа «три в ряд».

Если существование игры, подобной крестикам-ноликам, в Древнем Египте поставлено под вопрос, то можем ли мы быть уверены в том, что игра была знакома жителям Древнего Рима?

И тут всё не так плохо: есть письменный источник. Это, как ни странно, «Наука любви» (Ars Amatoria) Публия Овидия Назона — своеобразная древнеримская «Камасутра» начала I в. (не исключено, что в ссылку на Черноморское побережье Дакии Овидий угодил именно как автор этого «развратного» произведения). В ней Овидий советует девушкам научиться играть в различные игры, чтобы очаровывать мужчин. Правда, перечисляя эти игры, описанию каждой он отводит всего по одной-две строки. В написанных позже «Скорбных элегиях» он вновь упоминает игру с тремя фишками, но и здесь ограничивается парой строк, почти дословно повторяющих сказанное в «Науке любви». О самой игре из этих двух текстов понятно только, что у игроков есть по три фишки и их нужно выстроить в ряд на доске. При этом на территории, принадлежавшей Римской империи, найдено множество полей для такой игры, но их надёжная датировка затруднена. К счастью, одно такое поле нанесли на черепицу до обжига, и на той же черепице находится печать XXX легиона, что позволяет говорить о времени создания поля — не ранее 196 г. до н. э.

Однако некоторые неточности в отношении древнеримской версии игры всё-таки проникли в популярную литературу. Во-первых, Овидий нигде не приводит названия игры. Название Terni Lapilli — условное и используется для обозначения игры сегодня лишь потому, что Овидий упоминает три камешка (фишки). Из-за того что у Овидия не говорится о названии игры, её часто называют просто — «игра Овидия». Во-вторых, Овидий говорит о поле для игры tabella, а не использует термин tabula lusoria, который вообще применялся обычно к столикам для азартных игр. Ну и, наконец, вишенка на торте — современная реконструкция игры основана в большей мере на современных правилах похожих игр, потому что единственное, что мы знаем из Овидия: в игре следовало выстроить три фишки в ряд.

Сегодня игру, правила которой аналогичны «реконструированным правилам» Terni Lapilli, называют «трёхфишечной мельницей» [Three men’s morris], при этом в стандартную мельницу играют девятью фишками на доске из 24 полей. Только в английском у «мельницы» как минимум десять названий: nine-man morris, mill, mills, the mill game, merels, merrills, merelles, marelles, morelles и ninepenny marl.

Мюррей приводит ещё одну разновидность игры на поле 3 × 3 — в ней, после того как все фишки выставлены на доску, ходы осуществляются необязательно на соседние клетки, вместо этого фишка может быть перемещена на любую свободную клетку. Мюррей называет такой вариант игры «девять дырок» [nine holes]. В Гане распространена игра под названием «ачи» (achi), она похожа на «трёхфишечную мельницу», но у каждого игрока не три фишки, а четыре.

Но вернёмся к обычным крестикам-ноликам. В 1799 г. игра в крестики-нолики упоминается в белом стихе английского поэта «Озёрной школы» Уильяма Вордсворта, впрочем без указания названия игры:

Каких только не знали вы забот

И не чурались их! Однако ж были

У вас и праздники, и торжества,

И радости простые: вечерами,

Собравшись у каминного огня,

Как часто мы над грифельной доской

Склонялись низко друг напротив друга

И крестики чертили и нули

В баталиях упорных — впрочем, вряд ли

Их удостою описанья здесь^, .

Первая печатная ссылка на английское название игры — noughts and crosses (nought — альтернативное слово для обозначения нуля) — появилась в 1858 г. в выпуске журнала «Записки и запросы». В статье, подписанной «A. De Morgan», обсуждается возможность исчисления шахматной игры. Автор вспоминает игру, в которую играли его однокашники и которую одни называли noughts and crosses, а другие — tit-tat-toe (это были слова победителя в игре, подобно словам «шах и мат» в шахматах). Несложно догадаться, что подпись «A. De Morgan» принадлежит уже упоминавшемуся нами шотландскому математику и логику Огастесу де Моргану, благодаря жене которого, Софии Элизабет де Морган, мы знаем подробности одного из первых визитов Ады Лавлейс к Чарльзу Бэббиджу.

Считается, что первая печатная ссылка на игру с названием, похожим на современное американское tic-tac-toe, — tick-tack-toe — появилась в 1884 г., но тогда это слово обозначало игру, в которую играют на грифельной доске и которая состоит из попыток с закрытыми глазами попасть карандашом по одному из множества чисел, при этом число, на которое попал карандаш, становится числом очков в игре. Не исключено, что название tic-tac-toe происходит от названия старинной версии нардов — tick-tack. Считается также, что американское переименование noughts and crosses в tic-tac-toe произошло уже в XX в., однако, по-моему, tic-tac-toe — это простое фонетическое искажение упомянутого де Морганом tit-tat-toe.

Де Морган не был единственным мыслителем своего времени, задумавшимся над проблемой исчисления настольных игр. Автобиография Чарльза Бэббиджа, вышедшая в 1864 г., проливает свет на подробности проекта по строительству машины, способной играть в крестики-нолики.

Первоначально Бэббидж занимался задачей с философской точки зрения, исследуя вопрос, можно ли построить машину, способную играть в шахматы, шашки или крестики-нолики (Бэббидж использовал термин tit-tat-to). Сделав вывод о том, что это возможно, Бэббидж разработал алгоритм перебора всех возможных вариантов, с помощью которого машина могла бы выбирать наилучшие ходы. Кроме того, он пришёл к выводу, что его аналитическая машина вполне способна выполнять все необходимые для этого действия: «Весь вопрос о создании автомата, способного играть в любую игру, зависит от способности машины представлять все мириады комбинаций, связанных с ней. Допустив по сто ходов каждой из сторон в самой длинной партии в шахматы, я обнаружил, что число возможных комбинаций в аналитической машине во много раз превосходит все необходимые требования».

Затем Бэббидж сосредоточил усилия на самой простой из рассмотренных им игр. Он подсчитал количество ходов в игре и изучил вопрос о том, каким образом автомат может выполнять необходимые расчёты. После того как Бэббидж пришёл к выводу о возможности создания такой машины, он понял, что доходы, полученные от неё, можно использовать для финансирования более серьёзного проекта — аналитической машины. Однако после подробного анализа вопроса Бэббидж решил, что прогнозируемая прибыль будет слишком низкой, чтобы даже в случае финансового успеха компенсировать время и деньги, затраченные на разработку и производство автомата.

Записи Бэббиджа об автомате для игры в крестики-нолики датируются с 25 сентября 1844 г. по 24 октября 1868 г., причём большая часть работы над механизмами системы и алгоритмами принятия решений была завершена к концу 1848 г. Алгоритм поиска выигрышных ходов был полностью завершён к октябрю 1860 г. Однако реальная машина, способная играть в крестики-нолики, появилась лишь спустя почти сто лет — в 1950 г. Джозеф Кейтс создал для Канадской национальной выставки в Торонто «Берти Мозг» (Bertie the Brain) — машину четырёхметровой высоты, имевшую несколько уровней сложности и призванную продемонстрировать возможности аддитрона (additron) — новой миниатюрной версии радиолампы. Спустя два года Александр Дуглас создал OXO — реализацию крестиков-ноликов для компьютера EDSAC (Electronic Delay Storage Automatic Calculator) с графическим выводом на 6-дюймовую электронно-лучевую трубку. OXO стала, по всей видимости, первой игрой, разработанной для компьютера общего назначения.

С вычислительной точки зрения крестики-нолики представляют собой довольно простую задачу. Несложно прикинуть количество возможных позиций в игре: каждое из полей доски, состоящей из девяти клеток, может быть пустым либо содержать крестик или нолик. Таким образом, у нас есть девять полей, для каждого из которых существует три возможных состояния, следовательно, общее число позиций составляет 3⁹ = 19 683. Однако данное число включает в себя множество невозможных позиций, например позицию с пятью крестиками и без единого нолика. Более точный подсчёт позволяет сократить это число до 5478, а с учётом идентичности всех возможных поворотов и отражений остаётся лишь 765 действительно различных позиций.

Простая оценка верхней границы количества различных партий даёт нам 9! = 362 880 (первый ход можно сделать на одну из девяти свободных клеток, второй — на одну из оставшихся восьми и т. д.). Это число включает в себя некорректные игры, в которых ходы продолжались уже после победы одной из сторон. За вычетом таких ситуаций игр остаётся 255 168, а удаляя отражения и повороты, получаем всего 26 830 возможных партий. Даже для ранних ламповых компьютеров полный перебор такого количества вариантов не представлял большой сложности, то есть машина могла рассмотреть в любой позиции все возможные варианты продолжения игры и выбрать ход, который обеспечивает наилучший для машины результат даже при идеальной игре противника.

В 1960 г. Дональд Мичи разработал программу, получившую название «Спичечнокоробочный обучающийся движок для крестиков-ноликов» (Matchbox Educable Noughts And Crosses Engine, MENACE; слово menace по-английски значит «угроза»). Эта программа была способна обучиться идеальной игре в крестики-нолики и для своего выполнения не требовала такого дефицитного ресурса, как компьютер. Вместо него Мичи использовал набор из трёх сотен спичечных коробков, каждый из которых соответствовал уникальному состоянию доски. Спичечные коробки были заполнены цветными бусинками, соответствующими отдельным ходам. Количество шариков каждого цвета указывало на «уверенность» в том, что соответствующий ход является наилучшим. В зависимости от результата каждой сыгранной партии производилось изменение количества бусинок в коробках, соответствующих возникшим в игре позициям, в результате чего программа постепенно всё более уверенно выбирала правильные ходы. В статье Мичи, посвящённой MENACE, впервые был введён термин «обучение с подкреплением» [reinforcement learning].

Простота крестиков-ноликов сделала эту игру популярным модельным объектом на заре развития электронных вычислительных машин. В наши дни анализ этой игры удобен в педагогических целях: при помощи крестиков-ноликов удобно иллюстрировать многие положения классической теории игр, а создание программы, способной играть в эту игру, — неплохое упражнение для начинающих разработчиков систем искусственного интеллекта.

‎

Loading comments...