3.3.2 Метод обратной индукции

Часто приписываемый Цермело метод обратной индукции был впервые описан в 1944 г. в монографии Джона фон Неймана и Оскара Моргенштерна «Теория игр и экономическое поведение» [Theory of Games and Economic Behavior] , сегодня считающейся одной из основополагающих работ в области теории игр.

Значимость работ Джона фон Неймана для вычислительной техники трудно переоценить. Наверняка вы слышали, что архитектуру большинства современных компьютеров часто называют архитектурой фон Неймана (мы ещё вернёмся к этому термину позже), а сами компьютеры — фон-неймановскими машинами. Кроме того, фон Нейман заложил основы математического аппарата квантовой механики, внёс существенный вклад в теорию операторов (его именем назван особый вид алгебр — алгебры фон Неймана), предложил теорию клеточных автоматов, а также стал одним из ключевых участников Манхэттенского проекта. В 1970 г. Международный астрономический союз присвоил имя Джона фон Неймана кратеру на обратной стороне Луны. В его память учреждены следующие награды: медаль Джона фон Неймана, Теоретическая премия фон Неймана, «Лекция Джона фон Неймана».

Кем же был этот человек со звучной немецкой фамилией?

Янош Лайош Нейман родился в 1903 г. и был старшим из трёх сыновей в состоятельной еврейской будапештской семье. Его отец, Микса Нейман, переселился в Будапешт из маленького городка Печ в конце 1880-х гг. Он получил степень доктора юриспруденции и работал юристом в Венгерском ипотечно-кредитном банке (Magyar Jelzálog-Hitelbank). Мать Яноша, Маргарет Канн, была домохозяйкой и старшей дочерью коммерсанта Якоба Канна — партнёра в фирме Kann—Heller, торговавшей сельхозоборудованием.

Янош с детства проявлял признаки одарённости: в шесть лет он мог делить в уме восьмизначные числа, складывать фразы на древнегреческом, в восемь — уже неплохо разбирался в математическом анализе.

Дела Миксы Неймана шли довольно неплохо — основатель и глава банка Кальман Селль в 1899 г. получил пост премьер-министра Венгрии и хотя и пробыл на нём относительно недолго (до 1903 г.), но впоследствии сохранял видную позицию в венгерской элите.

В 1913 г. старшему Нейману был пожалован дворянский титул с правом наследования. Таким образом Янош получил дополнение к своему имени в виде символа знатности. Теперь его имя звучало по-австрийски как Янош фон Нейман, а по-венгерски как Нейман Маргиттаи Янош Лайош. Когда позже фон Нейман преподавал в Берлине и Гамбурге, его называли Иоганн фон Нейман. После переезда в 1930-х гг. в США, его имя изменилось на английский манер — Джон. Забавно, что братья фон Неймана, оказавшись в США получили совсем другие фамилии: Vonneumann и Newman.

Джон Харсаньи, венгерский эмигрант и представитель следующего поколения исследователей теории игр, хотя лично и не знал фон Неймана, но был хорошо знаком с обществом, из которого он вышел. Согласно Харсаньи, фон Нейман всегда использовал приставку «фон» к фамилии и его задевало, если кто-то опускал её. Более того, фон Нейман настаивал на том, что если предложение начиналось с его фамилии, то вы не должны были использовать заглавную букву в слове «фон», поскольку изменение первоначального написания недопустимо. Это, конечно, было весьма незначительной человеческой слабостью.

фон Нейман получил степень доктора философии по математике в Будапештском университете в 1926 г. Параллельно он изучал химические технологии в Швейцарской высшей технической школе Цюриха. Отец Яноша считал, что профессия математика не сможет обеспечить сыну надёжное будущее. В 1927 г. фон Нейман был назначен приват-доцентом Берлинского университета, став самым молодым обладателем этой степени в истории университета. Первую половину 1929/30 учебного года он провёл на должности приват-доцента в Гамбурге.

В 1930 г. фон Нейман был приглашён на преподавательскую позицию в Принстонский университет, а далее, с 1933 г. и до самой смерти, занимал профессорскую должность в уже знакомом нам Институте перспективных исследований (IAS).

В межвоенные годы многие европейские евреи эмигрировали в США, среди них был ряд венгерских учёных: помимо фон Неймана в США перебрались Теодор фон Карман, Пол Халмош, Юджин Вигнер, Эдвард Теллер, Дьёрдь Пойа, Денеш Габор и Пал Эрдёш, многие из них затем приняли участие в разработке ядерного оружия. Современники отмечали, что венгерские учёные обладали развитым интеллектом, говорили на необычном языке, а их родиной была сравнительно небольшая страна. В результате их стали в шутку называть марсианами, что сами учёные приняли с должным чувством юмора.

В соответствии с шуточной легендой венгерские учёные были потомками разведывательных сил Марса, которые якобы приземлились в Будапеште на рубеже XIX–XX вв. и от которых женщины зачали детей. Вскоре марсиане, посчитав планету непригодной для исследований и жизни, оставили Землю. Родившиеся якобы от марсиан дети позднее уехали в Америку.

Дьёрдь Маркс в книге «Прибытие марсиан» (A marslakók érkezése) писал:

— …Вселенная — огромная, содержит мириады звёзд, и многие из них не слишком отличаются от нашего Солнца. Вокруг многих из этих звёзд, возможно, вращаются планеты. Какая-то часть этих планет содержит жидкую воду на своей поверхности и газообразную атмосферу. Исходящая от звезды энергия приводит к синтезу органических веществ, превращает океан в тонкий слой тёплого супа. Эти химические вещества соединяются друг с другом и создают систему самопроизводства. Простейшие живые организмы размножаются, эволюционируют в ходе естественного отбора и становятся более сложными, пока не появятся по-настоящему мыслящие существа. Далее последуют цивилизация, наука и технология. И в поисках новых миров они отправятся на соседние планеты, а затем планеты у соседних звёзд. И они расселятся по всей галактике. И эти исключительно развитые люди уж точно не проглядят такое прекрасное место, как наша Земля. Итак, — Ферми подошёл к решающему вопросу, — если всё это произошло, то они уже наверняка прибыли сюда. Так где же они?

Именно Лео Силард, человек с отличным чувством юмора, дал идеальный ответ парадоксу Ферми:

— Они среди нас, — ответил он, — но называют себя венграми.

Итак, фон Нейман и Моргенштерн дали формальное математическое определение обратной индукции (заметим, что они не использовали этот термин как таковой, а говорили лишь об индукции и последовательном рассмотрении позиций игры в обратном порядке — от тривиальных к нетривиальным). Сам термин «обратная индукция» периодически использовался математиками и ранее, но современное его применение в качестве обозначения процедуры, предложенной фон Нейманом и Моргенштерном, начинает утверждаться только в начале 1950-х в работах отца динамического программирования Ричарда Беллмана.

В современной терминологии обратной индукцией называют метод нахождения оптимальной последовательности действий в игре, основанный на обратной хронологии: сначала определяется оптимальное действие на последнем шаге, затем на предпоследнем и так далее, а в последнюю очередь устанавливается то действие, которое нужно совершить в начале игры. В шахматах такой способ исследования позиции обычно называют ретроспективным (или ретроградным) анализом или же просто ретроанализом. Ещё до появления формального обоснования обратной индукции ретроанализ был отдельным жанром шахматной композиции, где для решения обычно необходимо восстановить ходы, которые привели к возникновению заданной позиции.

Методология динамического программирования, позволяющая машинам осуществлять ретроспективный анализ игр, была создана Беллманом в 1965 г. Публикация Беллмана стала итогом его работы, о которой сообщалось ещё четырьмя годами ранее. Беллман полагал, что рано или поздно появятся машины, способные, применяя его метод, найти полное вычислительное решение задачи оптимальной игры для шашек, в отношении же шахмат он считал, что удастся получить точные решения для некоторых классов окончаний — например для чисто пешечных эндшпилей.

Давайте рассмотрим пример применения метода ретроспективного анализа к такой простой игре, как крестики-нолики.

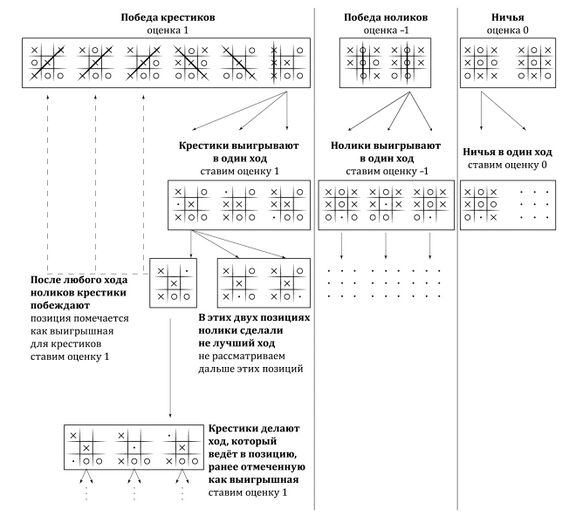
1. Для начала мы перечислим все возможные позиции и присвоим каждой из них неопределённую оценку, поскольку мы пока не знаем, какие из них являются выигрышными, проигрышными или ничейными. Затем присвоим оценку тем позициям, в которых на доске присутствует три крестика в ряд, — эти позиции выиграны крестиками, и мы с чистой совестью можем присвоить им соответствующую оценку, равную 1 (единицей мы будем обозначать победу крестиков). Аналогичную операцию проделаем с позициями, в которых в ряд выстроились три нолика, — этим, выигранным ноликами позициям мы присвоим оценку –1 (минус единица будет соответствовать позициям, выигранным ноликами). Затем настаёт очередь очевидно ничейных позиций, то есть таких позиций, в которых не осталось ни одного свободного поля, но при этом отсутствуют выстроившиеся в ряд по три крестики и нолики. Оценку таких позиций назначим равной 0, что будет соответствовать ничьей.
2. Теперь рассмотрим множество позиций с неопределённой оценкой, в которых очередь хода за крестиками и существует хотя бы один ход, ведущий в позицию с оценкой 1. Оценкой для таких позиций тоже становится единица: то есть позиции, в которых у крестиков есть хотя бы один ход, ведущий в выигрышную для них позицию, являются для них тоже выигрышными.
3. Аналогично для позиций с очередью хода, принадлежащей ноликам, имеющих неопределённую оценку, при наличии у ноликов хотя бы одного хода, ведущего в позицию с оценкой –1, устанавливаем оценку, равную –1.
4. Рассмотрим теперь позиции, для которых все возможные ходы приводят в позиции с определённой оценкой. Для таких позиций выберем оценку, соответствующую лучшему из возможных исходов для стороны, которой принадлежит очередь хода. То есть если очередь хода принадлежит крестикам и у них есть ход, ведущий в ничейную позицию, то оценкой позиции является 0, в противном случае (т. е. если все ходы ведут к проигрышным позициям) оценкой позиции становится –1. Если же очередь хода за ноликами и у них есть ход, ведущий в ничейную позицию, то оценкой позиции становится 0, в противном же случае — 1.
5. Если на шагах 2–4 была получена хотя бы одна новая оценка, возвращаемся к шагу 2.

Таким образом, мы, начав с финальных позиций игры, постепенно перемещаемся в направлении её начальной позиции, присваивая по пути оценки позициям промежуточным. Именно из-за этого движения задом наперёд метод называется ретроспективным анализом.

Работу алгоритмов удобно рассматривать в графической форме, используя представление игры в виде древовидной структуры, в которой узлы соответствуют позициям в игре, а ветви — возможным ходам. Алгоритм начинает работу с установления оценки для нижних (терминальных) узлов дерева, а затем постепенно поднимается вверх, пока не достигает корневого узла — начальной позиции игры.

Рис. 54. Метод ретроспективного анализа в применении к игре крестики-нолики

Если игра, подобно описанной Цермело версии шахмат, допускает достижение ничьей при помощи бесконечных последовательностей ходов, то описанный нами алгоритм по завершении работы оставит оценку для таких позиций неопределённой и нам достаточно будет просто заменить неопределённые оценки на нули, соответствующие ничьей, чтобы иметь определённые оценки для всех игровых позиций.

Получив точные оценки для всех позиций игры, мы можем использовать их для того, чтобы в любой позиции совершать идеальный ход. Достаточно просто просмотреть список всех возможных ходов в текущей позиции и выбрать тот, который ведёт в позицию с наилучшей для нас оценкой.

Таким образом мы и получаем введённые ранее Цермело заполненные множества последовательностей ходов.

‎

Loading comments...