3.5.2 Шахматные программы: без шахматных машин

Первая машина, способная играть в шахматы в полном соответствии со всеми правилами, появилась на свет почти через полвека после создания «шахматного игрока».

Но, что ещё интереснее, первая программа для игры в шахматы появилась задолго до того, как появилась машина, способная её выполнять! И ответственен за столь необычную веху в истории ИИ — Алан Тьюринг.

После окончания Второй мировой войны Тьюринг работал в Национальной физической лаборатории (NPL), где занимался разработкой одного из первых компьютеров — «Автоматического вычислительного механизма» (Automatic Computing Engine, ACE) — предшественника Manchester и Ferranti Mark I. В 1945 г. в отчёте Тьюринга под названием «Предлагаемый электронный калькулятор» упоминается десять задач, которые могли бы быть решены при помощи ACE; последней в списке значится программа для игры в шахматы. Идея была развита в 1948 г. в следующем отчёте под названием «Интеллектуальная техника», в котором Тьюринг упоминает проведённые им эксперименты в этом направлении. Считается, что первые идеи Тьюринга в отношении компьютерных шахмат относятся к 1941–1942 гг.

В конце лета 1948 г. Тьюринг вместе со своим коллегой Дэвидом Чемпернауном разработали алгоритм определения хода в шахматной игре на основе перебора вариантов. Однако он был слишком сложен для того, чтобы воплотить его в виде программы для ACE или любого другого компьютера того времени. Программа получила название «Тьюрочемп» (Turochamp), составленное из первых букв фамилий авторов. Вооружившись карандашом и бумагой, авторы выполняли необходимые расчёты за машину вручную — на выбор одного хода уходило около 30 минут. Этот аттракцион получил название «бумажной машины». «Бумажная машина» оказалась способна обыграть начинающего игрока — жену Чемпернауна, но проиграла Алику Гленни, создателю первого в истории компилятора — Autocode. Партия «бумажной машины» против Гленни продолжалась 29 ходов и сохранилась до наших дней.

Хотя Чемпернаун в 1980 г. и описал алгоритм работы программы в письме в редакцию журнала Personal Computing, некоторые детали за три десятилетия стёрлись из памяти учёного. К счастью, до нас дошло достаточно подробное описание алгоритма Turochamp, подготовленное самим Тьюрингом для вышедшего в 1953 г. сборника «Быстрее мысли: симпозиум по цифровым вычислительным машинам» (Faster than Thought: A Symposium on Digital Computing Machines) под редакцией Бертрама Баудена. Текст, набранный на печатной машинке, содержит собственноручные пометки и исправления Тьюринга. Выбор хода в программе Тьюринга и Чемпернауна был основан на переборе вариантов на фиксированную глубину. При этом варианты со взятиями рассматривались в глубину вплоть до позиций, в которых ни одно взятие было невозможно. Оценочная функция Turochamp оценивала материал (конь оценивался в три пешки, слон — в три с половиной, ладья — в пять и ферзь —в десять пешек), мобильность фигур, а также некоторое количество других позиционных признаков.

В 2004 г., основываясь на имеющихся материалах, Фредерик Фридель — известный научный журналист, многолетний редактор журнала Computerschach und Spiele (Компьютерные шахматы и игра) и сооснователь компании ChessBase, — заручившись поддержкой одного из ведущих разработчиков ChessBase Матиаса Файста, воссоздал Turochamp в виде работающей программы. Таким образом, спустя более чем полстолетия программа Тьюринга наконец обрела компьютерное «тело».

В процессе работы над Turochamp команда ChessBase столкнулась с проблемой: программа отказалась повторять все ходы, записанные Тьюрингом в игре против Гленни. Исследователи потратили несколько недель на повторное изучение материалов Тьюринга и обсуждение особенностей их реализации. К работе команды подключился Кен Томпсон, который написал собственный код на основе инструкций Тьюринга. Но и его программа вела себя сходным образом и повторяла большую часть ходов программы ChessBase, отличавшихся от ходов Тьюринга в партии.

В чём же было дело? Были ли это ошибки Тьюринга или неточности реконструкторов?

Фридель связался с Дональдом Мичи, работавшим с Тьюрингом в Блетчли-парке, описал суть проблемы и рассказал о наиболее существенных расхождениях между ходами в партии и ходами программы. «Возможно, мы делаем что-то не так, — писал Фридель, — но я сомневаюсь в этом, поскольку очень часто, особенно в начале игры, мы получаем те же ходы с одинаковыми оценками. Думаю, вполне возможно, что Тьюринг устал после пятнадцати ходов, когда вдобавок ко всему позиция стала достаточно сложной?!» Реакция Мичи была следующей: «Вы ищете ошибку в программе, Фредерик? Нет-нет, вы должны искать её у Алана Тьюринга! Алан не заботился о деталях; его интересовал общий принцип». Он также привёл слова Чемпернауна, который помогал Тьюрингу в создании «бумажной машины»: «В натурном эксперименте, я подозреваю, мы были слегка небрежны и наверняка наделали множество ошибок, поскольку расчёты были чрезвычайно утомительны при использовании карандаша и бумаги».

Результаты работы по воссозданию Turochamp были представлены на конференции, прошедшей в Блетчли-парке 23 июня 2012 г. и посвящённой столетию со дня рождения Алана Тьюринга. Вместе с Фриделем на конференции выступил тринадцатый чемпион мира по шахматам Гарри Каспаров, который провёл короткую демонстрационную партию против Turochamp — играя чёрными, он выиграл её за 16 ходов.

До своей трагической смерти в 1954 г. Тьюринг так и не успел реализовать Turochamp в виде программного кода, но эстафету подхватили другие исследователи. Вообще говоря, шахматы с самого начала рассматривались в качестве своеобразного священного Грааля машинного интеллекта — эта традиция берёт истоки ещё в работах Бэббиджа. Конрад Цузе, работая над своим языком программирования Plankalkül, анализировал задачу определения валидности шахматных ходов и разработал для этого ряд программных процедур^, . В 1950 г. опубликована написанная двумя годами ранее программная статья Клода Шеннона «Программирование компьютера для игры в шахматы», в которой сформулированы основные подходы к созданию шахматных программ, в значительной мере определившие развитие шахматного программирования в последующие полстолетия.

В целом идеи, изложенные Шенноном в статье, во многом пересекаются с идеями Тьюринга. Шеннон также предлагает использовать оценочную функцию, принимающую в расчёт материал, мобильность, отдельные элементы пешечной структуры: слабые, изолированные и сдвоенные пешки, нахождение ладей на открытых вертикалях и некоторые другие широко известные признаки, используемые шахматистами при оценке позиции. Интересно, что Шеннон предлагает немного отличающиеся значения для оценки фигур (у Тьюринга слон стоит три с половиной пешки, а у Шеннона — три, как и конь). Шеннон также пишет о том, что перебор в узле дерева можно прерывать только в «спокойных» [quiescent] позициях, поскольку значение оценочной функции бессмысленно в середине цепочки разменов. Если при переборе в глубину на три полухода белые третьим полуходом взяли чёрного ферзя, то программа может посчитать результатом соответствующего варианта выигрыш ферзя, хотя в действительности чёрные заберут «лишнего» ферзя белых следующим ходом, тем самым уравняв позицию. Термин quiescent, употреблённый Шенноном, и в наши дни используется для обозначения в шахматных программах функций, отвечающих за анализ форсированных вариантов, например: quiescence_search() или просто quiescence(). Шеннон по сути приводит в статье свой вариант этой функции: он предлагает продолжать перебор в течение нескольких дополнительных полуходов, если хотя бы одна фигура на доске атакована более слабой фигурой, либо атакована недостаточно защищённая фигура, либо существует возможность дать шах на незащищённое поле.

Вообще статья Шеннона интересна в первую очередь как раз анализом задачи перебора вариантов. Шеннон описывает две программы — тип A и тип B. Программа типа A просматривает дерево игры на фиксированную глубину, при этом в каждом узле дерева (соответствующем позиции на доске) рассматриваются все возможные ходы соответствующей стороны. Такой подход гарантирует нахождение любой игровой комбинации, если глубина рассмотрения дерева достаточна для этого. Однако дерево шахматной игры, особенно в миттельшпиле, ветвится чрезвычайно быстро. В среднестатистической шахматной позиции возможно примерно 35 различных полуходов, что более чем в десять раз превосходит аналогичный показатель для английских шашек. Оценив вычислительные возможности машин, Шеннон делает неутешительный вывод: программа типа A вряд ли когда-либо сможет сравниться с лучшими шахматистами, ведь некоторые комбинации чемпионов мира насчитывают 15–20 ходов в глубину! В качестве альтернативы программе типа A Шеннон предлагает программу типа B, которая будет рассматривать в каждом узле дерева игры не все, а только некоторые альтернативы — это позволит увеличить глубину рассмотрения дерева за счёт уменьшения его ширины. Похожим образом действуют и профессиональные шахматные игроки — включают в рассмотрение только те варианты, которые считают осмысленными.

Дьявол, однако, как обычно, кроется в деталях. В 1950 г. в арсенале методов ИИ ещё не было инструментов, позволявших получить оценку «осмысленности» того или иного варианта, сопоставимую по качеству с человеческой. Да что уж говорить — даже самого ИИ как направления ещё не существовало. Программа типа B, руководствуясь примитивными способами отсеивания вариантов, неизбежно часто допускала бы грубые ошибки, эту проблему видел и Шеннон. Последовавшие десятилетия развития шахматных программ во многом стали поиском разумного компромисса между полным и селективным, избирательным перебором вариантов, а также поиском быстрых и в то же время умных оценочных функций.

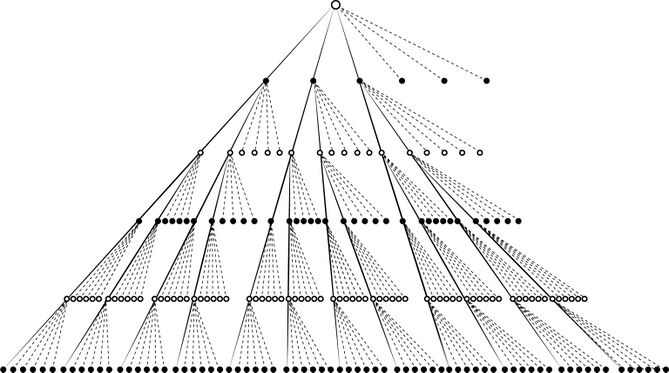
В своей работе Шеннон рассматривает возможность ограничения количества вариантов, анализируемых на каждом из уровней дерева перебора. Например, на картинке ниже изображено дерево с ограничениями числа рассматриваемых вариантов в 3, 2, 2, 1, 1 для глубины соответственно в 1, 2, 3, 4 и 5 полуходов. Сплошными линиями показаны «разрешённые» к рассмотрению ходы, штриховыми — «запрещённые».

Рис. 65. Дерево перебора с ограничением числа рассматриваемых вариантов в каждом узле (программа типа B)

Количество рассматриваемых вариантов на этой схеме зависит только от глубины и не зависит от качества соответствующей позиции и самих ходов — это, конечно, серьёзное упрощение. В действительности Шеннон предлагал разработать некоторую функцию h(P, M), где P — позиция, а M — ход, для определения того, достоин ли ход рассмотрения в данной позиции. Шеннон даже выполнил некоторые наброски такой функции: предложил присваивать большие значения шахам, развивающим ходам, взятиям, атакам на фигуры, угрозам мата и так далее.

В статье Шеннона обнаружилось достаточно деталей для того, чтобы уже знакомый нам Матиас Файст создал на её основе «программу Шеннона». Инго Альтхофер из Йенского университета в 2012 г. организовал демонстрационный матч из десяти партий, в котором «программа Тьюринга» сразилась с «программой Шеннона». Итогом матча стала ничья — каждая из программ выиграла по одной партии, а остальные восемь завершились миром. До последней партии «Тьюринг» лидировал, но последнюю выиграл «Шеннон», сравняв счёт. Причиной поражения «Тьюринга» стал эффект горизонта. Также в ходе матча выяснилось, что ни одна из программ не способна поставить «голому» королю мат ни ладьёй, ни даже ферзём.

Сегодня исходные коды «воссозданных» программ Тьюринга и Шеннона, так же как и, например, исходные коды программы, основанной на отдельных идеях Конрада Цузе, размещены в открытом доступе. Однако важно понимать, что все они содержат некоторый произвол со стороны реконструкторов, ведь ни одна из этих программ не существовала в действительности, а дошедшие до нас документы допускают в ряде случаев весьма широкое пространство для трактовок и домыслов.

Интересно, что Turochamp не была единственной «бумажной машиной» того времени. В 1947–1948 гг. уже знакомый нам Дональд Мичи совместно с другим криптоаналитиком из Блетчли-парка Шоном Уайли создали программу, а точнее, алгоритм, получивший название «Макиавелли» (Machiavelli). Это имя он получил в честь знаменитого итальянского мыслителя, писателя и политического деятеля эпохи Возрождения Никколо Макиавелли. В начале 1950‑х гг. Тьюринг вёл работы по превращению Turochamp и Machiavelli в программы для манчестерских компьютеров, но эта работа так и осталась незавершённой. Исторические Machiavelli и Turochamp так и не сыграли ни одной партии, пока до них не добрались неутомимые реконструкторы.

В статье «Машины, которые играют в игры», увидевшей свет в 1961 г., Джон Мейнард Смит и Дональд Мичи описали оценочные функции своих алгоритмов — SOMA (Smith One-Move Analyzer, «Одноходовый анализатор Смита») и Machiavelli. Обе «бумажные машины» предполагали анализ вариантов всего на один полуход в глубину, поэтому вряд ли могли обыграть кого-то, кроме шахматных новичков. Функции оценки включали в себя подсчёт материала, контроль над центром доски и полями, соседствующими с королём, атаки на фигуры, оценки разменов и ряд других стратегических и тактических факторов. Позже Смит создал гибрид SOMA и Machiavelli, получивший название SOMAC. Этот алгоритм при переборе в глубину на два полухода обеспечивал уровень игры, соответствующий среднему шахматному игроку-любителю.

‎

Loading comments...