4.2.5 Два английских джентльмена и долгопёрый прибрежный кальмар

Дальнейшее развитие идей Лапика в рамках вычислительной нейробиологии привело к появлению множества более точных и полных моделей биологического нейрона. В их числе модели «интегрировать-и-сработать с утечками» [leaky integrate-and-fire], «интегрировать-и-сработать с утечками дробного порядка» [fractional-order leaky integrate-and-fire], модель Гальвеса — Лёхербах [Galves–Löcherbach model], «экспоненциальный вариант модели „интегрировать-и-сработать“» [exponential integrate-and-fire] и многие другие. Поскольку погружение в пучины вычислительной нейробиологии стоило бы нам нескольких сотен страниц, переполненных формулами и экспериментальными данными, мы остановимся здесь только на одном из ключевых исследований в этой области, обойти которое никак нельзя — тем более что его авторы в 1963 г. получили за него Нобелевскую премию в области физиологии и медицины. Речь, разумеется, об исследованиях сэра Алана Ходжкина, ученика Эдриана, и сэра Эндрю Хаксли. Эти два почтенных английских джентльмена навсегда останутся в истории науки благодаря тому, что любили резать кальмаров не только за ужином, но и на протяжении всего рабочего дня.

Интересно, что Эндрю Хаксли был не только братом другого знаменитого биолога, Джулиана Хаксли, одного из основателей Синтетической теории эволюции, не только братом знаменитого писателя Олдоса Хаксли (подарившего миру знаменитый роман-антиутопию «О дивный новый мир»), но и внуком Томаса Гексли, известного учёного-эволюциониста и популяризатора науки, получившего прозвище Бульдог Дарвина. Как вы уже, наверное, догадались, Гексли и Хаксли — это одна и та же фамилия, которую в разные годы по-разному записали по-русски.

Рис. 81. Долгопёрый прибрежный кальмар

Долгопёрый прибрежный кальмар (Doryteuthis pealeii), как и другие кальмары, является чрезвычайно удобным для нейрофизиологов модельным организмом благодаря наличию у него гигантских аксонов.

Гигантский аксон кальмаров — это очень большой (обычно около 0,5 мм в диаметре, но иногда достигает 1,5 мм) аксон, который контролирует часть водореактивной системы кальмара, используемой им в основном для коротких, но очень быстрых перемещений в воде. Впервые гигантский аксон описан Леонардом Уильямсом в 1909 г., однако это открытие было забыто более чем на двадцать лет, вплоть до исследований английского зоолога и нейрофизиолога Джона Янга в 1930-е гг.

Между щупальцами кальмара расположен сифон, через который вода может быстро выталкиваться за счёт сокращений мышц стенки тела животного. Это сокращение инициируется потенциалами действия в гигантском аксоне. Поскольку электрическое сопротивление обратно пропорционально площади поперечного сечения объекта, потенциалы действия распространяются быстрее в большем аксоне, чем в меньшем. Поэтому увеличение диаметра гигантского аксона поддерживалось в процессе эволюции, так как позволяло увеличить скорость мышечной реакции.

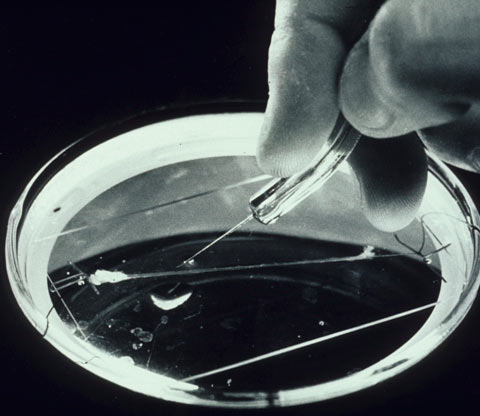
Это стало настоящим подарком для Ходжкина и Хаксли, которых интересовал ионный механизм потенциалов действия, — ведь благодаря большому диаметру аксона в его просвет можно было невозбранно установить электроды!

Рис. 82. Гигантский аксон кальмара

В итоге учёные создали модель Ходжкина — Хаксли, но для её рассмотрения надо вначале поговорить о механизмах, лежащих в основе нервной проводимости.

Мембрана (оболочка) нейрона поляризована. Это означает, что существует постоянная разность потенциалов между внутренней и наружной поверхностью клеточной мембраны. Эта разность получила название «мембранный потенциал». Мембранный потенциал нейрона в обычном состоянии («потенциал покоя») отрицателен и у млекопитающих равен примерно −70 мВ. Смещение мембранного потенциала в отрицательную сторону относительно потенциала покоя называется гиперполяризацией, а в положительную — деполяризацией. Под воздействием слабых (подпороговых) импульсов электрического тока в клетке возникает «электротонический потенциал», то есть сдвиг мембранного потенциала клетки, вызываемый действием постоянного электрического тока. Передача импульса по нервным волокнам происходит в виде волны возбуждения, в основе которой лежат электротонические потенциалы и потенциалы действия, которые распространяются вдоль нервного волокна.

В участках нервного волокна, изолированных миелиновыми оболочками, распространение электрических импульсов происходит очень быстро, скачкообразно. Почему это происходит, позволяет понять школьный курс физики. Электрический ток — это направленный поток частиц — носителей электрического заряда в проводнике. Такими частицами в случае металлов являются электроны, а в случае электролитов — ионы. Цитоплазма нейронов — это электролит, в котором функцию переноса зарядов выполняют различные типы ионов. Вообще говоря, этих типов ровно четыре: положительно заряженные ионы калия, кальция и натрия и отрицательно заряженные ионы хлора. Пока разность потенциалов на разных концах изолированного проводника отсутствует, заряженные частицы движутся хаотически, в разных направлениях. Как только возникает разность потенциалов на одном из концов проводника, частицы практически мгновенно выстраиваются в цепочку, благодаря чему тут же возникает разность потенциалов на втором конце изолированного проводника. Распространение электрического сигнала тем самым происходит со скоростью света, что куда быстрее скорости перемещения самих заряженных частиц в проводнике. Например, скорость движения электронов в металлическом проводнике составляет доли миллиметра в секунду (величина этой скорости зависит от величины разности потенциалов), а скорость распространения электрического тока — порядка 300 000 км/с.

Однако в случае, когда проводник не изолирован или изолирован плохо, скорость распространения сигнала сильно падает из-за утечек. Мембраны нейронов содержат молекулярные механизмы, отвечающие за регуляцию разности потенциалов между внутренним пространством клеток и внешней средой. Это ионные насосы (помпы) и ионные каналы.

Ионные насосы — специальные белки, которые обеспечивают активный перенос ионов из области с меньшей концентрацией в область с большей концентрацией за счёт энергии гидролиза аденозинтрифосфорной кислоты (АТФ). Именно в результате работы ионных насосов создаётся и поддерживается разность концентрации ионов по обе стороны мембраны (так называемый трансмембранный ионный градиент).

Ионные каналы — белки (или белковые комплексы), которые обеспечивают пассивный транспорт ионов из области с большей концентрацией в область с меньшей концентрацией как раз за счёт разности концентраций. Ионные каналы делятся на селективные и неселективные. Последние всегда находятся в открытом состоянии и пропускают все типы ионов (при этом их проницаемость для положительно заряженных ионов кальция значительно выше, чем для других ионов). Селективные каналы пропускают только один вид ионов — для каждого вида ионов существует свой вид каналов. При этом селективные каналы могут находиться в одном из трёх состояний: активированном, инактивированном и закрытом.

Кроме того, в зависимости от способа управления, ионные каналы подразделяются на потенциал-зависимые (потенциал-управляемые), лиганд-зависимые (лиганд-управляемые), стимул-управляемые, неуправляемые, а также некоторые другие, на которых мы не будем заострять особого внимания.

Потенциал-зависимые ионные каналы открываются и закрываются в ответ на изменение мембранного потенциала. Лиганд-зависимые каналы открываются, когда вещество-нейромедиатор, связываясь с их наружными рецепторными участками в синаптической щели, меняет их конформацию (т. е. пространственное расположение атомов в молекуле). Стимул-управляемые каналы открываются ввиду действия какого-либо стимула и бывают механочувствительные, протон-активируемые, температурно-чувствительные и так далее. Что касается неуправляемых каналов, то они, как можно догадаться из их названия, постоянно находятся в открытом состоянии^, .

Однако даже и в изолированном миелином нервном волокне электрический сигнал постепенно затухает. Поэтому, чтобы компенсировать этот эффект, и требуются упомянутые ранее перехваты Ранвье. Они выполняют роль своеобразных «трансформаторных подстанций», усиливающих сигнал до необходимого уровня. Таким образом, электрический импульс в миелинизированных волокнах перескакивает от одного перехвата к другому, чтобы получить в нём очередное подкрепление. Такой механизм хорошо объясняет экспериментальные результаты, полученные Эдрианом, Като и их коллегами.

Возможность быстрой передачи нервных сигналов по миелинизированным нервным волокнам стала важным эволюционным преимуществом позвоночных организмов, увеличив скорость их мышечной реакции на внешние раздражители и позволив им увеличиваться в размерах. В наши дни учёные продолжают изучение механизмов действия перехватов Ранвье. Например, исследуются механизмы, связанные с влиянием на их функции инфракрасного излучения^, . Не исключено, что дальнейшие исследования помогут ещё лучше уточнить детали устройства тонкой биохимической и биофизической «машинерии».

Теперь можно наконец и рассмотреть модель Ходжкина — Хаксли. Она представляет собой систему нелинейных дифференциальных уравнений, которая приближённо описывает электрические характеристики возбуждаемых клеток. Модель сопоставляет каждому компоненту клетки его физический аналог, рассматривая его в качестве элемента электрической цепи.

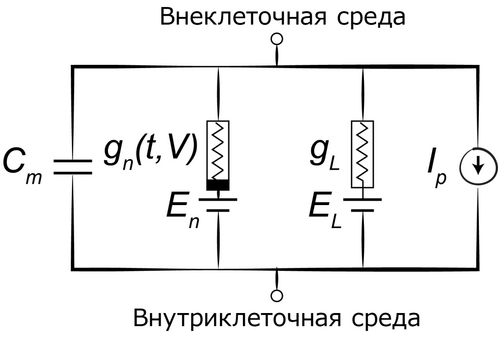
Рис. 83. Электрическая схема, соответствующая модели Ходжкина — Хаксли

Внутреннему липидному слою клеточной мембраны соответствует электроёмкость C_m. Потенциал-зависимые ионные каналы обеспечивают нелинейную электропроводность g_n (где n — отдельный вид ионных каналов), зависящую от величины потенциала и времени. Эта часть системы, как было обнаружено в более поздних исследованиях, базируется на белковых молекулах, образующих потенциал-зависимые ионные каналы. Вероятность открытия канала зависит от электрического потенциала (или электрического напряжения) мембраны клетки. Как мы уже знаем, каналы мембранных пор обеспечивают пассивный переток ионов в направлении области с их меньшей концентрацией. Участок цепи, соответствующий электропроводности g_L, отвечает как раз за возникающий в результате этого электрический ток, называемый «током утечки» (L от англ. leak — течь, утечка). Разность концентрации ионов, ввиду которой ионы перемещаются через мембранные каналы, показана на схеме при помощи источников напряжения с электродвижущей силой E_n и E_L. Ионные насосы соответствуют источникам тока I_p.

Модель Ходжкина — Хаксли считается одним из величайших достижений биофизики XX в. Со временем она подверглась модификациям и улучшениям. На базе экспериментальных данных в модель были добавлены новые виды ионных каналов и транспортёров. Модель была модифицирована с целью её согласования с теорией переходного состояния, что привело к созданию термодинамических моделей Ходжкина — Хаксли. Создание стохастических (т. е. связанных со случайностью, от греческого слова στοχαστικός — умеющий угадывать) моделей поведения ионных каналов привело к появлению стохастических гибридных систем, в которых детерминистические описания непрерывной динамики сочетаются со скачкообразными марковскими процессами, а также модели Пуассона — Нернста — Планка (PNP) для моделирования процессов ионного обмена в каналах. Дело в том, что ионные каналы — это весьма сложные приспособления, для моделирования которых необходимо учитывать самые разные физические и химические эффекты. Здесь есть место как для электрохимии, так и для гидродинамики. Через каждый канал может проходить от миллиона до 100 млн ионов в секунду, при этом на открытие или закрытие канала уходит всего порядка миллисекунды, и оно может происходить под влиянием разных механизмов, а на активность работы канала оказывает влияние несколько модулирующих факторов^, . Именно поэтому модели, учитывающие все особенности работы ионных каналов, являются весьма сложными.

Учёными было разработано несколько упрощённых моделей нейронов (таких как модель Фитцхью — Нагумо или модель Ижикевича), облегчающих эффективное крупномасштабное моделирование их групп. Кроме того, современные модели обычно подразумевают наличие разветвлённой структуры аксонов и дендритов.

Loading comments...