4.4.8 Теоретические результаты

Итогом работы Розенблатта и его коллег, помимо практических, стал ряд важных теоретических результатов. К их числу относятся, в частности, формулировка и доказательство теоремы о сходимости перцептрона. Как и теореме Цермело, теореме Розенблатта не слишком повезло, поскольку многие современные источники содержат неверную или избыточную формулировку теоремы. Тем, кто интересуется формальной математической стороной вопроса, я рекомендую небольшое расследование, проделанное на эту тему Леем Мао, а мы попробуем взглянуть на сформулированную Розенблаттом проблему в более неформальном ключе.

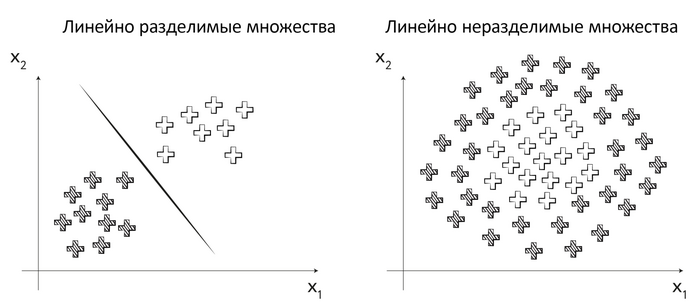
Любую задачу классификации с произвольным числом классов можно свести к решению одной или нескольких задач, в которых число классов равно двум. Например, если у нас есть задача распознавания на картинке котиков, собак и енотов, то мы можем представить её в виде совокупности двух задач: задачи «отличать котиков от всех прочих животных» и задачи «отличать собак от енотов». Воспользовавшись этой особенностью задач классификации, мы будем рассматривать задачу с двумя классами. Её можно легко представить в графической форме. Для этого нужно взять n-мерное евклидово пространство, где n — количество факторов, задействованных в задаче (т. е. при одном факторе это будет числовая прямая, при двух факторах — плоскость, при трёх — трёхмерное пространство и т. д.), и отобразить в нём известные нам прецеденты (элементы обучающей выборки) в виде точек двух цветов (скажем, красных и зелёных). В случае задачи с двумя факторами мы получим множество красных и зелёных точек на плоскости. Если зелёные точки можно отделить от красных, проведя на плоскости некоторую прямую (для большего числа факторов — проведя в пространстве некую гиперплоскость), то множества красных и зелёных точек называют линейно разделимыми.

Рис. 98. Примеры линейно разделимых и линейно неразделимых множеств

Перцептрон, имеющий только один слой нейронов с настраиваемыми синаптическими весами, является линейным классификатором, то есть в процессе обучения он пытается найти гиперплоскость, разделяющую прецеденты, относящиеся к различным классам. Смысл теоремы о сходимости перцептрона заключается в том, что (как удалось доказать Розенблатту) такой однослойный перцептрон, обучаемый при помощи метода коррекции ошибки, всегда, независимо от стартового состояния синаптических весов и последовательности поступления элементов обучающей выборки, достигнет решения за конечный промежуток времени — то есть для линейно разделимых классов решение всегда будет найдено за конечное количество шагов обучения. Кроме того, Розенблатт рассчитал верхний предел количества таких шагов. Помимо теоремы о сходимости перцептрона, Розенблатт также представил доказательства ряда смежных теорем, связанных с архитектурой искусственных нейронных сетей и методами их обучения.

Впрочем, первые кирпичики в математический фундамент коннекционизма, как это ни странно, были заложены математиками, казалось бы далёкими от проблематики искусственных нейронных сетей. Речь идёт о решении так называемой тринадцатой проблемы Гильберта советскими математиками Владимиром Арнольдом и Андреем Колмогоровым. Гильберта интересовал вопрос о том, можно ли представить решение общего уравнения седьмой степени в виде суперпозиции непрерывных функций двух переменных. Арнольду и Колмогорову удалось доказать эту проблему в более общем виде, результатом чего стало появление теоремы Арнольда — Колмогорова, которая гласила: любая многомерная непрерывная функция может быть представлена в виде суперпозиции непрерывных функций одной переменной. В некотором роде советские математики показали, что единственная «истинная» функция многих переменных — это сложение, поскольку все другие функции можно записать с использованием функций одной переменной и сложения. Но ведь искусственная нейронная сеть как раз и представляет собой сочетание сложения, которое выполняют нейроны, и подстановки, которой соответствует передача сигнала через синаптическую связь. Таким образом, из теоремы Арнольда — Колмогорова следует, что абсолютно любая многомерная непрерывная функция может быть реализована при помощи искусственной нейронной сети.

Этот результат был довольно неожиданным, поскольку, согласно ему, вся сложность многомерных функций может быть сведена к тривиальным операциям одномерных функций. В результате становится возможным использование методов групповой подстройки множеств однородных параметров для моделирования плохо формализуемых механизмов и процессов.

Статьи Колмогорова и Арнольда были опубликованы в СССР в 1956–1957 гг., но английские их версии появились в печати только в начале 1960-х гг. Поэтому Розенблатт, начиная свою работу над перцептронами, скорее всего, ничего не знал о неожиданном и обнадёживающем результате, полученном советскими математиками. И всё-таки именно ему, скромному нейрофизиологу, а вовсе не математикам и информатикам удалось оказаться в нужное время в нужном месте и стать на некоторое время лидером нового направления в науке, обильные плоды которого мы пожинаем в наши дни. Розенблатт был в некотором роде математиком поневоле, его практические эксперименты нередко оказывались впереди попыток строгого математического обоснования методов, лежащих в их основе. Да и сами математические выкладки Розенблатта, по мнению некоторых специалистов, не всегда были корректны. И всё-таки именно в руках этого худощавого юноши в очках были рабочий образец самообучающейся машины и обнадёживающие результаты экспериментов.

Фрэнк Розенблатт был весьма разносторонней личностью. Будучи руководителем отдела когнитивных систем в Корнелле, он читал лекции на факультете психологии. Его курс под названием «Теория механизмов мозга» был рассчитан на студентов как инженерных, так и гуманитарных факультетов и включал в себя огромное число сведений из различных областей знаний. Здесь были и результаты, полученные во время операций на мозге больных эпилепсией (при нахождении пациентов в сознании), и эксперименты по изучению активности отдельных нейронов зрительной коры кошек (речь идёт о работах Дэвида Хьюбела и Торстена Визеля — их мы обсудим более подробно немного позже), и работы по изучению изменений в протекании психических процессов в результате травм различных областей мозга, принципы работы различных электронных устройств, моделирующих поведение биологических нейронных сетей (в том числе перцептрона).

Несмотря на то что в те годы в арсенале нейронауки не было ещё таких современных методов, как компьютерная и позитронно-эмиссионная томография, Розенблатт смог дать вполне адекватные оценки возможностей человеческого мозга. Например, основываясь на доступных ему данных, он произвёл серию вычислений и пришёл к выводу, что нейронных связей в коре головного мозга человека достаточно для того, чтобы хранить точные «фотографические» образы, поступающие от органов зрения со скоростью 16 кадров в секунду, в течение не менее двухсот лет.

Именно на основе этого курса была написана книга «Принципы нейродинамики», которую Розенблатт использовал затем в качестве учебника для студентов.

Loading comments...