Перейти к содержанию

5.2.3.4 Теория расчёта весов и описание метода обратного распространения ошибки

Материал из Охота на электроовец: Большая Книга Искусственного Интеллекта

Теперь, когда мы обсудили историю возникновения этого метода, самое время познакомиться с ним поглубже.

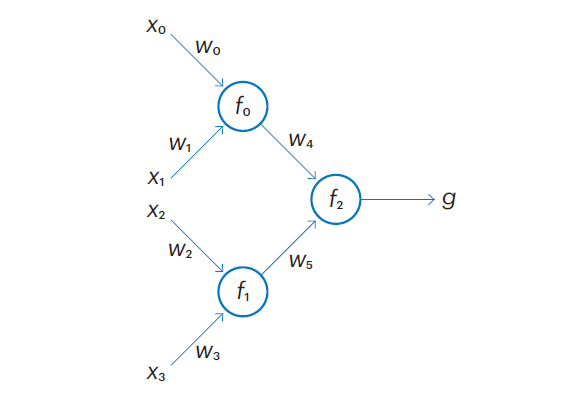
В целом задача поиска направления наибольшего убывания ошибки в пространстве весов нейронной сети соответствует задаче поиска направления коррекции каждого из синаптических весов и степени влияния изменения этого веса на величину ошибки. Любую нейронную сеть можно представить в виде алгебраического выражения, описывающего функцию ответа сети на полученные её рецептивным (входным) слоем входы. В простейшем варианте, когда сеть состоит из одного нейрона, это выражение будет иметь вид g(x0,x1,…,xn)=f(∑inwixi), где x0…xn — входы сети, w0…wn — веса входных синапсов нейрона, а f — функция его активации. То есть все входы перемножаются на соответствующие веса, суммируются, а затем подставляются в функцию активации, значение которой и будет выходом нашего нейрона. Если одним из входов нашего нейрона является, в свою очередь, выход другого нейрона, то вместо соответствующей переменной xi мы должны будем подставить выражение, описывающее этот нейрон. Представим себе сеть из трёх нейронов:

Функция ответа такой сети будет иметь вид g(x0,x1,x2,x3)=f2(w4f0(w0x0+w1x1)++w5f1(w2x2+w3x3)), то есть мы подставили выражения f0(w0x0+w1x1) и f1(w2x2+w3x3), описывающие нейроны входного слоя, в выражение, описывающее нейрон второго слоя. По мере увеличения числа нейронов и синапсов эта формула будет становиться всё более и более огромной, но общий принцип будет оставаться неизменным. Трудно вообразить формулу, описывающую сеть из миллиона нейронов, но нет никаких сомнений в том, что при наличии необходимого числа карандашей, бумаги, свободного времени, слабоумия и отваги её всё-таки можно записать. Несложно сообразить, что, обладая формулой, позволяющей рассчитать ответ нейронной сети при заданном наборе входных данных, можно также составить функцию для расчёта ошибки этой сети для одного прецедента, для некоторого набора прецедентов, да даже для всей обучающей выборки. Например, в случае задачи с распознаванием слонов по массе и длине тела мы можем использовать сумму квадратов разниц ответов сети и действительных значений метки. Несложно заметить, что если наша сеть выдаёт только нули и единицы, то величина такой функции ошибки будет представлять собой количество случаев, в которых сеть выдала ответ, не соответствующий действительной метке класса. Если же наша сеть способна выдавать какие-либо величины, отличные от нулей и единиц, то такая функция ошибки позволит нам оценить близость выдаваемых сетью ответов к правильным меткам. Если все функции активации нейронной сети непрерывны и дифференцируемы, то есть имеют производную (хотя бы в текущей точке, но в идеале на всём пространстве параметров), значит дифференцируемой будет и наша функция ошибки, ведь суперпозиция дифференцируемых функций также является дифференцируемой. Следовательно, мы можем вычислить частные производные функции ошибки вдоль всех осей пространства весов нейронной сети. При расчёте частной производной все веса, кроме того, который соответствует расчётной оси, принимаются за константы, а затем применяется цепное правило для вычисления производной композиции функций.

Алгоритм обратного распространения ошибки заключается в последовательном расчёте частных производных послойно: начав с выходного слоя сети, он переходит к предпоследнему слою, затем к предшествующему ему слою и так далее. Движение в обратном направлении позволяет избежать избыточных вычислений промежуточных членов в цепном правиле и по сути представляет собой применение метода динамического программирования к вычислительному графу.

Полный набор частных производных составляет так называемую матрицу Якоби [Jacobian matrix], получившую своё имя в честь немецкого математика Карла Густава Якоба Яко́би. Каждая из частных производных определяет уклон функции ошибки в направлении соответствующей оси пространства весов сети, поэтому матрица Якоби описывает вектор направления наибольшего возрастания (а взятая с противоположным знаком — убывания) функции. Знание этого направления позволяет применить широкий арсенал методов градиентного спуска, суть которых сводится к движению в пространстве параметров модели в поиске точки с минимальным значением ошибки.

Метод обратного распространения ошибки, строго говоря, относится только к алгоритму вычисления градиента, а не к тому, как затем будет использоваться полученный градиент. Однако в современной литературе это понятие нередко применяется для обозначения всего алгоритма обучения, из-за чего возникает некоторая путаница, которой мы постараемся избежать.

Используемые в наши дни на практике алгоритмы градиентного спуска содержат множество нюансов, описание которых выходит далеко за границы этой книги, но всё же обратим внимание на некоторые из них.

Во-первых, смещение в пространстве поиска может происходить с разным шагом. Этот шаг представляет собой скалярный коэффициент, на который домножается градиент функции ошибки для вычисления смещения относительно текущей точки. Этот коэффициент принято называть скоростью обучения [learning rate]. Слишком маленькое значение скорости обучения может приводить к излишне медленному движению в сторону минимума, а также к попаданию в локальные минимумы. Вообще, локальные оптимумы являются одним из главных проклятий задач нелинейной оптимизации, ведь целевая функция совершенно не обязана быть монотонной. Если вы выйдете из своего дома и будете двигаться в направлении наибольшего уклона поверхности вниз, то, скорее всего, закончите свой путь в ближайшем овраге, а вовсе не на дне Марианской впадины, являющейся наиболее глубокой точкой на поверхности Земли.

Скорость обучения — это длина вашего шага. Если ваши шаги будут микроскопическими, то вы, скорее всего, застрянете в ближайшей выемке на асфальте. С другой стороны, слишком большие шаги могут привести к тому, что вы просто проскочите глобальный минимум. Современные алгоритмы оптимизации обычно постепенно изменяют скорость обучения. Например, на старте обучения размер шага может постепенно возрастать (этот процесс называют «разогревом» [warmup]), а затем плавно сокращаться, иногда в зависимости от изменения величины целевой функции, — в таком случае говорят об «адаптивной скорости обучения» [adaptive learning rate].

Во-вторых, распространённым трюком для борьбы со сваливанием в локальный минимум является так называемый «момент». Его проще всего понять как аналогию инерции движущегося объекта — вы не просто идёте в направлении наибольшего уклона поверхности, но и обладаете некоторой инерцией, которая позволяет вам «проскакивать» небольшие неровности. Вместо моментов первого порядка (матрицы Якоби) было бы неплохо использовать моменты второго порядка, так называемую матрицу Гессе [Hessian matrix], названную так в честь другого немецкого математика XIX в. — Людвига Отто Гессе. Использование моментов второго порядка, то есть не просто направления наибольшего изменения функции, а направления наибольшего изменения самого этого уклона, обещает более быструю сходимость. На деле вычисление моментов второго порядка связано с большими вычислительными затратами, поэтому было изобретено множество способов их приблизительного расчёта.

Важной особенностью алгоритмов оптимизации является выбор множества прецедентов, используемых для расчёта ошибки. Ошибка может быть рассчитана на всём множестве прецедентов обучающей выборки. Но в этом случае количество прецедентов очень велико и вычислительный граф, используемый для представления получившейся в итоге циклопической функции ошибки, оказывается слишком большим. В результате он может просто не вместиться в оперативную память машины, что приведёт к фатальному замедлению процесса обучения.

Другой крайностью может быть использование для расчёта ошибки случайно выбранного единичного прецедента из обучающей выборки. Но в этом случае полученное значение ошибки может слабо коррелировать с величиной ошибки на всей выборке в целом — обобщения, основанные лишь на одном примере, чаще всего являются некорректными. Кроме того, современные вычислительные машины устроены таким образом, что многие вычисления они более эффективно производят «оптом». Как и в промышленном производстве, эти современные вычислительные фабрики обеспечивают более низкую себестоимость единицы продукции тогда, когда их производственные мощности загружены на 100%. Поэтому на деле данные обучающей выборки обычно «скармливаются» нейронной сети в виде пакетов, содержащих в себе случайные подмножества прецедентов. Такие пакеты называют «мини-батчами» [mini batch] или просто «батчами». Случайное разбиение обучающей выборки на батчи, а также случайный порядок обработки батчей позволяют алгоритмам оптимизации более эффективно справляться с проблемой локальных минимумов, чем в случае с расчётом градиента на базе всей обучающей выборки. Даже если в ходе оптимизации мы оказались в таком минимуме, всегда есть шанс, что текущая точка уже не будет таким локальным минимумом для другого батча. Оптимальный размер батча зависит от конкретной задачи оптимизации, в частности от степени однородности данных в обучающей выборке (чем однороднее данные, тем величина ошибки для случайно отобранного батча будет более точным приближением для величины ошибки на всей обучающей выборке). Некоторые современные алгоритмы оптимизации могут использовать при обучении переменный размер батча, в ряде случаев это позволяет улучшить сходимость. Поскольку батч, используемый на очередном шаге оптимизации, выбирается случайным образом[1], то алгоритмы, использующие данный подход, относятся к числу методов «стохастического градиентного спуска» (Stochastic Gradient Descent, SGD). Наиболее ранними алгоритмами данного семейства стали алгоритмы Роббинса — Монро (Robbins—Monro)[2] и Кифера — Вольфовитца (Kiefer—Wolfowitz)[3], созданные соответственно в 1951 и 1952 гг., разумеется, безо всякой связи с нейронными сетями. С 1960-х гг. различные варианты SGD использовались для обучения линейных регрессионных моделей, а с 1980-х — для обучения искусственных нейронных сетей. В уже упомянутой нами статье Румельхарта, Хинтона и Уильямса 1986 г.[4] содержатся предложения об усовершенствовании стохастического градиентного спуска путём добавления так называемого момента, или, как правильнее было бы сказать по-русски, импульса (от англ. momentum — импульс). Это дополнение часто называют также методом тяжёлого шара, что отсылает нас к интуитивно понятному примеру из физического мира. Представим себе процесс оптимизации как качение массивного шара по поверхности целевой функции. Скатываясь вниз в направлении уклона, наш шар будет по инерции проскакивать локальные минимумы, поскольку обладает некоторым импульсом. Эту идею классики машинного обучения позаимствовали из написанной в 1964 г. статьи[5], [6] советского математика Бориса Поляка, посвящённой решению функциональных уравнений. Данный подход был позже доработан советским и бельгийским математиком Юрием Нестеровым и сегодня является частью многих современных вариантов SGD.

В наши дни для обучения нейронных сетей применяется множество различных алгоритмов стохастического градиентного спуска: AdaGrad[7], ADADELTA[8], RMSProp[9], Adam[10], Nadam[11], AdamW[12], Adan[13], Neograd[14], NovoGrad[15], Adai[16], Shampoo[17], Distributed Shampoo[18], Sophia[19], Lion[20] и так далее. Их количество сегодня уже перевалило за сотню[21].

Выбор наилучшего оптимизатора сильно зависит от особенностей конкретной задачи, и, к сожалению, не существует универсального рецепта на все случаи жизни. Кроме того, успех оптимизации может сильно зависеть от выбора начальной точки (или множества начальных точек), поэтому отдельным важным вопросом является вопрос об инициализации весов нейронной сети. В начале процесса обучения сети её веса обычно инициализируют псевдослучайными значениями, но какими должны быть параметры распределения этих значений? Должны ли они быть одинаковыми во всех слоях или же должны каким-то образом зависеть от глубины слоя? Как это ни странно, от ответа на этот, казалось бы, второстепенный вопрос в действительности зависит многое.

  1. ↑ * На деле, конечно, псевдослучайным, поскольку источниками «случайности» чаще всего являются генераторы псевдослучайных чисел.
  2. ↑ Robbins H., Monro S. (1951). A Stochastic Approximation Method. / Annals of Mathematical Statistics, Vol. 22, Iss. 3, pp. 400—407, September, 1951 // https://doi.org/10.1214/aoms/1177729586
  3. ↑ Kiefer J., Wolfowitz J. (1952). Stochastic Estimation of the Maximum of a Regression Function. / Annals of Mathematical Statistics, Vol. 23, Iss. 3, September, 1952, pp. 462—466 // https://doi.org/10.1214/aoms/1177729392
  4. ↑ Rumelhart D. E., Hinton G. E., Williams R. J. (1986). Learning representations by back-propagating errors / Nature, 323(6088), pp. 533–536 // https://doi.org/10.1038/323533a0
  5. ↑ Поляк Б. Т. (1964). О некоторых способах ускорения сходимости итерационных методов. / Журнал вычислительной математики и математической физики, том 4, номер 5, 1964, с. 791—803 // https://www.mathnet.ru/rus/zvmmf7713
  6. ↑ Polyak B. T. (1964). Some methods of speeding up the convergence of iteration methods. / USSR Computational Mathematics and Mathematical Physics, Vol. 4, Iss. 5, 1964, pp. 1—17 // https://doi.org/10.1016/0041-5553(64)90137-5
  7. ↑ Duchi J., Hazan E., Singer Y. (2011). Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. / Journal of Machine Learning Research 12 (2011) 2121-2159 // https://www.jmlr.org/papers/volume12/duchi11a/duchi11a.pdf
  8. ↑ Zeiler M. D. (2012). ADADELTA: An Adaptive Learning Rate Method // https://arxiv.org/abs/1212.5701
  9. ↑ Tieleman T., Hinton G. (2012). Lecture 6.5 - rmsprop: Divide the gradient by a running average of its recent magnitude // https://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf
  10. ↑ Kingma D. P., Ba J. (2014). Adam: A Method for Stochastic Optimization // https://arxiv.org/abs/1412.6980
  11. ↑ Dozat T. (2016). Incorporating nesterov momentum into Adam. / In International Conference on Learning Representations Workshops, 2016 // https://cs229.stanford.edu/proj2015/054_report.pdf
  12. ↑ Loshchilov I., Hutter F. (2017). Decoupled Weight Decay Regularization // https://arxiv.org/abs/1711.05101
  13. ↑ Xie X., Zhou P., Li H., Lin Z., Yan S. (2022). Adan: Adaptive Nesterov Momentum Algorithm for Faster Optimizing Deep Models // https://arxiv.org/abs/2208.06677
  14. ↑ Zimmer M. F. (2020). Neograd: Near-Ideal Gradient Descent // https://arxiv.org/abs/2010.07873
  15. ↑ Ginsburg B., Castonguay P., Hrinchuk O., Kuchaiev O., Lavrukhin V., Leary R., Li J., Nguyen H., Zhang Y., Cohen J. M. (2019). Stochastic Gradient Methods with Layer-wise Adaptive Moments for Training of Deep Networks // https://arxiv.org/abs/1905.11286
  16. ↑ Xie Z., Wang X., Zhang H., Sato I., Sugiyama M. (2020). Adai: Separating the Effects of Adaptive Learning Rate and Momentum Inertia // https://arxiv.org/abs/2006.15815
  17. ↑ Gupta V., Koren T., Singer Y. (2018). Shampoo: Preconditioned Stochastic Tensor Optimization // https://arxiv.org/abs/1802.09568
  18. ↑ Anil R., Gupta V., Koren T., Regan K., Singer Y. (2021). Scalable Second Order Optimization for Deep Learning // https://arxiv.org/abs/2002.09018
  19. ↑ Liu H., Li Z., Hall D., Liang P., Ma T. (2023). Sophia: A Scalable Stochastic Second-order Optimizer for Language Model Pre-training // https://arxiv.org/abs/2305.14342
  20. ↑ Chen X., Liang C., Huang D., Real E., Wang K., Liu Y., Pham H., Dong X., Luong T., Hsieh C.-J., Lu Y., Le Q. V. (2023). Symbolic Discovery of Optimization Algorithms // https://arxiv.org/abs/2302.06675
  21. ↑ Schmidt R. M., Schneider F., Hennig P. (2020). Descending through a Crowded Valley - Benchmarking Deep Learning Optimizers // https://arxiv.org/abs/2007.01547
Loading comments...
Источник — http://wiki.markoff.science/index.php?title=5.2.3.4_Теория_расчёта_весов_и_описание_метода_обратного_распространения_ошибки&oldid=1171