5.2.5.2 Предложения и проблемы

В университетском курсе по искусственному интеллекту две фамилии непрестанно следуют друг за другом: Элман и Джордан, Джордан и Элман. Прямо как Бивис и Баттхед — в наши дни их почти невозможно встретить поодиночке. О сетях Элмана и Джордана, в силу их архитектурного сходства, всегда рассказывают в одной лекции, для них даже изобретено обобщающее название — простые рекуррентные нейронные сети (Simple recurrent neural network, SRNN).

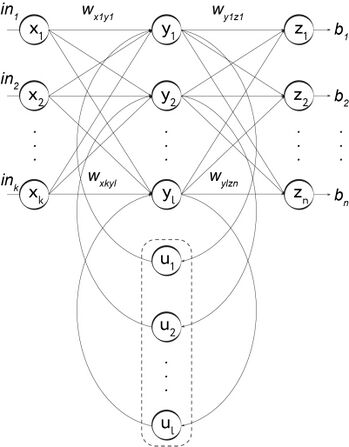
И всё-таки, несмотря на название, сети Элмана и Джордана не так уж просты, в их основе лежит определённая регулярная структура. От простой рекуррентной сети можно было бы ожидать наличия у неё полносвязной рекуррентной архитектуры — например, это могла бы быть полносвязная сеть с одним промежуточным слоем, в которой каждый нейрон промежуточного слоя, помимо связи с нейронами выходного слоя, имел бы рекуррентную связь с каждым другим нейроном промежуточного слоя. Такая сеть вполне ожидаемо называется полносвязной рекуррентной нейронной сетью (Fully connected recurrent neural network, FCRNN). Эти сети обычно не представляют особого интереса для исследователей, и из редких исследований, посвящённых полносвязной рекуррентной архитектуре, мы можем узнать немногим более одного вполне очевидного факта — обучение такой сети требует очень больших вычислительных затрат.

Рис. 104. Полносвязная рекуррентная нейронная сеть

Идея сети Элмана заключается в том, чтобы к обычной нерекуррентной полносвязной сети с l нейронами (и Элман и Джордан используют для нейронов термин «единицы», «блоки» [units], что подчёркивает тот факт, что речь в данном случае идёт не о биологических нейронах) в ассоциативном слое добавить ещё l специальных нейронов состояния [state neurons]. Каждый из этих нейронов связан с соответствующим ему нейроном ассоциативного слоя парой связей — прямой и обратной. Таким образом, на каждом шаге каждый ассоциативный нейрон будет с некоторым весом получать вход от соединённого с ним нейрона состояния, а затем с некоторым весом передавать в него свой выход. Фактически нейроны состояния в данном случае выполняют роль памяти модели.

Рис. 105. Сеть Элмана

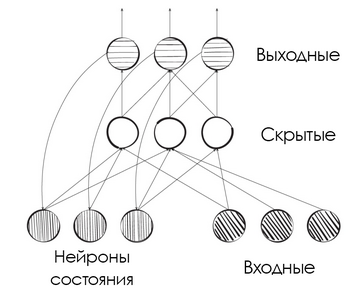
Сеть Джордана отличается от сети Элмана только тем, что нейроны рекуррентного слоя получают входы не от нейронов ассоциативного слоя, а от нейронов выходного слоя сети. Таким образом, в рекуррентный контур включаются не два нейрона (ассоциативный и рекуррентный), а три (ассоциативный, выходной и рекуррентный).

Важно отметить, что сети Элмана и Джордана часто изображают в виде неполных диаграмм, включающих в себя не все имеющиеся в них связи. Начало этой порочной практике положили сами авторы — диаграмма, приведённая в статье Джордана, содержит в подписи соответствующее предупреждение. Чтобы избежать путаницы, автор приводит отдельную табличку, в которой перечислены все имеющиеся в сети связи. Все нейроны сети Джордана (как и сети Элмана) разделены на четыре группы: плановые [plan], нейроны состояния [state], скрытые [hidden] и выходные [output]. Плановые нейроны и нейроны состояния в сумме составляют входные нейроны сети, такая группировка использована, по всей видимости, для того, чтобы подчеркнуть порядок выполняемых сетью вычислений. Давайте вместе попробуем разобраться в табличке Джордана.

Обзор соединительных структур сети

	Плановые элементы	Элементы состояния	Скрытые элементы	Выходные элементы
Плановые элементы			×	×
Элементы состояния		×	×	×
Скрытые элементы				×
Выходные элементы		×

В ячейке таблицы знак «×» стоит тогда и только тогда, когда нейроны, тип которых указан в заголовке столбца, получают входы от нейронов, тип которых указан в первой ячейке строки. Плановые нейроны, являясь рецептивными нейронами сети, получают входы только извне сети, поэтому первый столбец таблицы пуст. Каждый из нейронов состояния получает входы от выходных нейронов, а также от опять же нейронов состояния и так далее.

Если внимательно взглянуть на диаграмму сети, представленную Джорданом, можно отметить один интересный нюанс — наличие связей, соединяющих одни нейроны состояния с другими. Если подумать, то такая структура соединений вполне ожидаема, ведь нейроны состояния в некотором роде являются следующим слоем для самих себя, поэтому структура их связей с собой же повторяет, например, структуру связей между нейронами скрытого и выходного слоёв. В тексте статьи Джордан отмечает, что «рекуррентные связи между выходными блоками и блоками состояния не являются необходимыми для работы сети при наличии соединений между блоками состояния». Эта ремарка Джордана показывает, что, по сути, его работа вводит в оборот не одну, а несколько возможных архитектур сетей. В общем, копаясь в манускриптах древних, можно найти множество занятных подробностей.

Не менее, чем вопрос о топологии рекуррентных сетей, интересен вопрос: каким образом такие сети могут быть обучены? Трюки, позволяющие применять метод обратного распространения ошибки к рекуррентным сетям, изобретались разными исследователями неоднократно. Наверное, самый популярный из них получил название «метод обратного распространения ошибки сквозь время» [backpropagation through time]. Идея заключается в том, чтобы развернуть рекуррентную сеть вдоль временно́й шкалы, дублируя её для каждого момента времени и заменяя рекуррентные связи на прямые, соединяющие сеть, относящуюся к моменту времени t, с копией сети, относящейся к моменту времени t + 1. Однако применение этого метода на практике обнажает ахиллесову пяту метода обратного распространения ошибки — «проблему исчезающего (или затухающего) градиента» [vanishing gradient problem]. Поскольку производные сигмоидальных функций на краях достаточно малы, абсолютный размер ошибки (а значит, и величин коррекции весов сети) быстро уменьшается по мере удаления слоя, для которого производится расчёт, от выходного слоя сети. В принципе, эта проблема характерна не только для сигмоидальных функций, поскольку в процессе обратного распространения ошибки градиент для каждого i-го слоя рассчитывается на базе градиента для i + 1-го слоя, отдельные компоненты градиента могут легко стать слишком малыми величинами. Таким образом, острота проблемы растёт по мере увеличения количества слоёв обучаемой сети. В случае развёрнутой на множество шагов во времени рекуррентной сети, как и в случае других сверхглубоких архитектур, мы неизбежно будем сталкиваться с ситуацией, когда точности выбранного для хранения весов типа данных перестанет хватать для хранения сверхмалых компонент градиента. И даже если мы сможем преодолеть эту проблему, скажем за счёт использования специальных типов, скорость обучения такой сети будет, скорее всего, неудовлетворительной, ведь синаптические веса в передних слоях сети будут корректироваться крайне медленно. Вообще, градиенты весов нейронных сетей штука чрезвычайно капризная — при некоторых условиях они могут не только исчезать, но и, напротив, «взрываться» [exploding gradient problem]. Взрывающиеся или затухающие градиенты могут привести к стагнации или, напротив, слишком быстрому изменению синаптических весов и тем самым сделать обучение нейронной сети нестабильным. Поэтому архитекторы нейронных сетей нередко вынуждены применять для решения подобных проблем особую «уличную магию», например «обрезку градиента» [gradient clipping], уже упоминавшиеся нами «перепрыгивающие связи» и так далее.

Из-за проблемы исчезающего градиента на границе 1980–1990-х гг. исследователи могли позволить себе рекуррентные сети, способные различать лишь сравнительно короткие зависимости в обрабатываемых последовательностях^, . Было трудно поверить в то, что когда-нибудь появятся сети, способные улавливать закономерности в событиях, разделённых десятками или даже сотнями шагов. Однако через некоторое время появилась новая нейросетевая архитектура, способная существенно снизить остроту этой проблемы. О ней мы и поговорим в следующем разделе.

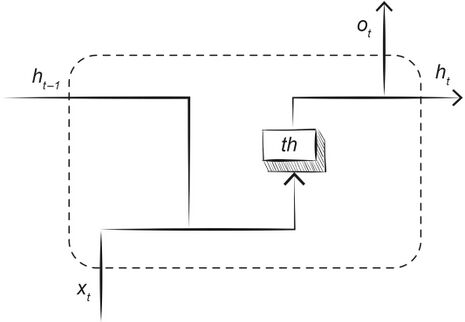
Рис. 106. Схематическое изображение блока рекуррентной нейронной сети (RNN). Обозначения: h_t−1 — предыдущее скрытое состояние, h_t — текущее скрытое состояние, x_t — обрабатываемый элемент последовательности, o_t — текущий выход, th — функция активации (гиперболический тангенс)

Loading comments...