5.2.6 Автокодировщики, контрастное обучение и близнецы Барлоу

Истратил я зарплату на новый пылесос.

Шумит как экскаватор, свистит как паровоз.

Вся пыль в него влетает с ковров и со стены…

И тут же вылетает с обратной стороны.

Павел Рудаков и Вениамин Нечаев. С обратной стороны

Современный прогресс в машинном обучении трудно представить без ещё одного важного класса нейросетевых моделей, а именно без автокодировщиков [autoencoder], которых также называют автоэнкодерами или иногда — автоассоциаторами.

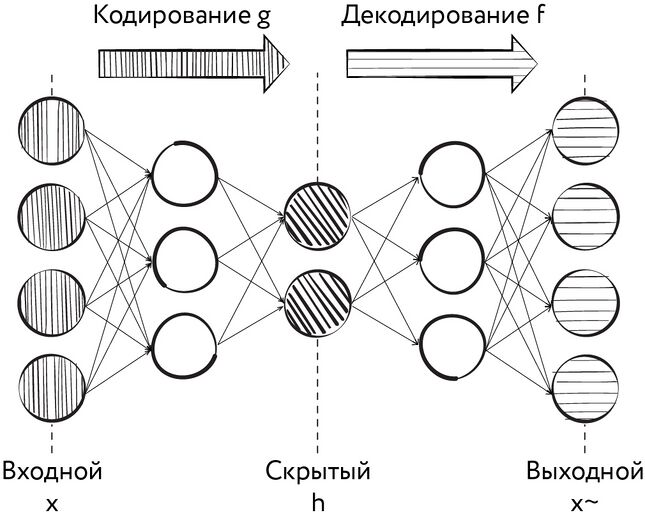
Обсуждая в начале книги типы задач, решаемых при помощи методов машинного обучения, мы упоминали задачу сокращения размерности. Например, словесное описание объекта куда компактнее фотографии, сделанной с высоким разрешением, однако по этому описанию можно, пусть и с некоторыми потерями, восстановить внешний вид описанного объекта. Представьте себе многослойную нерекуррентную нейронную сеть, в которой размерность рецептивного слоя в точности равна размерности выходного слоя. При этом слой, находящийся в середине сети, обладает существенно меньшей размерностью (либо при обучении такой сети используются какие-либо штрафы или ограничения для значений в этом слое). Например, на вход сети подаётся изображение размером 100 × 100 пикселей, стало быть, в её рецептивном слое, как и в выходном, 10 000 нейронов. В промежуточном же слое сети всего 500 нейронов. Мы будем обучать эту сеть таким образом, чтобы изображение, полученное на выходе сети, было максимально похоже на изображение, подаваемое на вход. Важной особенностью такой процедуры обучения является отсутствие учителя: данные, используемые для обучения автокодировщика, в общем случае не требуют разметки. Предъявив автоэнкодеру в ходе обучения десятки или сотни тысяч изображений, мы таким образом вынудим сеть придумать такой способ компактного представления картинок, который позволит добиться минимальных потерь в изображении при последующем его декодировании. При этом часть сети, начинающаяся с рецептивного слоя и заканчивающаяся самым узким слоем (своеобразным «бутылочным горлышком»), будет выполнять функцию кодировщика, а часть сети, начинающаяся с самого узкого слоя и заканчивающаяся выходным слоем, — роль декодера. Совокупность сигналов в нейронах самого узкого слоя, при поступлении на вход некоторого образа, называется латентным вектором [latent vector] или латентным представлением [latent representation] образа, а пространство возможных значений латентного вектора — латентным пространством. Описанная нами нейронная сеть называется, как вы уже, наверное, догадались — автокодировщиком.

Рис. 109. Схема автокодировщика

Сама архитектура связей такой сети может быть различной. Например, для обработки изображений чаще всего применяют свёрточные автокодировщики, то есть на входе такой модели присутствуют слои свёртки, а на выходе — обратные им по выполняемой функции слои развёртки. При обработке последовательностей могут использоваться рекуррентные автокодировщики. Ничто не мешает использовать и полносвязные архитектуры, архитектуры с какими-то особенными вычурными слоями.

Почему и за счёт чего автокодировщики работают? На этот вопрос можно ответить по-разному, но важно, что на практике данные, обрабатываемые при помощи автоэнкодеров, содержат некоторую избыточность, они отличаются от равномерно распределённого шума. В них присутствуют закономерности, которые и учится выявлять автокодировщик в процессе обучения.

Чем могут быть полезны автокодировщики? Конечно, первое напрашивающееся применение — это сжатие данных с потерями. Однако потенциальная польза от автокодировщиков куда шире. Автокодировщик может применяться в качестве генеративной модели. Например, обучив его на большом наборе фотографий людей, можно затем сгенерировать латентный вектор случайным образом, подставить его в декодер и получить совершенно новое фото (для таких задач в наши дни обычно используются так называемые вариационные автокодировщики (Variational Autoencoders, VAE) или методы вроде «состязательно ограниченных интерполяций автокодировщиков» (Adversarially Constrained Autoencoder Interpolation), которые накладывают некоторые дополнительные ограничения на латентные векторы автокодировщика, чтобы улучшить сходимость модели и качество генерируемых данных). Латентные векторы автокодировщика могут быть входом для моделей, решающих задачи классификации и регрессии — ведь компоненты такого вектора представляют собой, по сути дела, набор абстрактных признаков образов, использованных при обучении автоэнкодера. Потратив единожды вычислительные ресурсы на обучение автокодировщика, можно затем «недорого» строить множество «лёгких» моделей, решающих широкий спектр задач.

В начале нашего тысячелетия автокодировщики применялись для каскадного обучения глубоких сетей. Этот метод, предложенный Джеффри Хинтоном и Русланом Салахутдиновым, заключается в том, что слои нейронной сети обучаются последовательно слева направо. К очередному необученному слою на время обучения подключается декодер, дополняющий сеть до архитектуры автокодировщика. Затем полученный автокодировщик обучается, причём веса в уже обученных ранее слоях на время обучения фиксируются, этот приём называется заморозкой [freezing]. Описанная процедура повторяется для всех слоёв сети, кроме последних, которые обучаются в обычном режиме — с учителем и с применением метода обратного распространения ошибки. В наши дни этот способ обучения глубоких сетей применяется редко, поскольку были найдены другие, более удобные для практического применения способы борьбы с исчезновением градиента. Однако в отдельных случаях послойное предобучение всё-таки позволяет добиться наилучших результатов.

Также автоэнкодеры могут применяться для очистки сигнала от шума, в таком случае используют термин «шумоподавляющие автокодировщики» (Denoising Autoencoders, DAE). При обучении такого автокодировщика мы можем добавлять на вход сети некоторый шум, стремясь на выходе получить образ до внесения в него шума.

К латентному пространству автокодировщика можно присоединить какую-либо семантическую информацию относительно входного образа, например возраст человека на фото или наличие у него бороды. Затем, на этапе работы декодера, можно подменить эти значения другими, тем самым заставив сеть изменить возраст человека на фото или пририсовать ему бороду. Нередко отдельные компоненты латентного представления сами по себе в результате обучения оказываются интерпретируемыми параметрами: их смысл можно обнаружить, наблюдая изменения, происходящие с образом при изменении отдельных компонентов латентного вектора. Словом, значение автокодировщиков для республики машинного обучения огромно. Их вклад в достижение WOW-эффекта от многих демонстраций возможностей современных технологий искусственного интеллекта трудно переоценить.

Разобраться в том, кто именно изобрёл автокодировщики, не так уж просто. Сама идея сокращения размерности данных не нова. Ещё в 1901 г. Карл Пирсон, основатель математической статистики, предложил свой знаменитый метод главных компонент (Principal component analysis, PCA) — один из наиболее популярных «классических» способов уменьшения размерности данных с потерей наименьшего количества информации. Первые коннекционистские модели, адресующие эту проблему, появились в начале 1980-х. Ими стали самоорганизующиеся карты Кохонена (Self-organizing map, SOM) — одна из разновидностей сетей Кохонена. Их создатель, финский учёный, специалист в области искусственных нейронных сетей и машинного обучения Теуво Кохонен, опубликовал в 1981–1984 гг. первые работы, посвящённые развитию своей модели^{, ,} .

В 1984 г. Экли, Хинтон и Сейновски предложили решение, в котором набор входных образов сопоставляется с набором выходных образов через небольшой набор скрытых нейронов. В последующем году появилась публикация, посвящённая исследованию методов обучения такой сети.

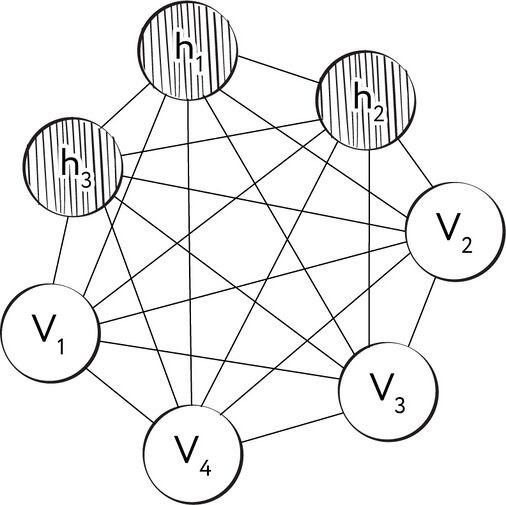
Эта модель и получила название «машина Больцмана», в честь австрийского физика Людвига Больцмана, одного из основоположников статистической физики. Все синаптические связи между нейронами больцмановской машины — симметричные, а сами нейроны разделены на два множества — скрытые и видимые, где последние выполняют роль рецептивного слоя. Каждый нейрон может находиться в одном из двух состояний — «включённом» [on] и «выключенном» [off], причём это состояние он приобретает на основе некоторой функции вероятности от состояний нейронов, соединённых с нашим нейроном, и от синаптических весов этих связей. Синаптические веса являются действительными числами и могут принимать также и отрицательные значения. Довольно интересно здесь то, что авторы статьи не говорят о том, какая именно функция вероятности может быть использована в машине, что позволяет конструировать машины Больцмана на основе самых разных функций. Понятно, что классическим решением будет логистическая функция от суммы произведений состояний связанных нейронов (где «включённое» состояние соответствует 1, а «выключенное» — 0) на веса соответствующих связей. Каждый нейрон также имеет индивидуальную величину «смещения» [bias] (иногда также используется термин «порог» [threshold]), обозначаемую традиционно буквой θ. Смещение можно рассматривать как вес синапса, связывающего наш нейрон с особенным нейроном, находящимся в постоянно включённом состоянии.

Хинтон и его коллеги рассматривали машину Больцмана как модель для решения задачи «удовлетворения ограничений» [constraint satisfaction], то есть задачи поиска набора значений переменных, удовлетворяющих определённому набору ограничений.

Рис. 110. Схема машины Больцмана

В математической статистике модели, подобные машине Больцмана, называют марковскими случайными полями.

Впрочем, достижением Хинтона и его коллег стало не только и не столько создание прямого нейросетевого аналога случайных марковских полей и присвоение ему имени австрийского физика (тем более что некоторые исследователи склонны рассматривать машину Больцмана в качестве разновидности сети Хопфилда), сколько идея использования для обучения таких сетей так называемого алгоритма имитации отжига [simulated annealing].

Название этого алгоритма отсылает нас ВНЕЗАПНО к металлургии, в которой отжигом называется вид термической обработки стали, заключающийся в нагреве заготовки до определённой температуры, выдержке в течение некоторого времени и последующем, обычно медленном, охлаждении до комнатной температуры. Из школьного курса физики мы знаем, что температура вещества пропорциональна средней кинетической энергии составляющих его частиц. Чем выше температура, тем быстрее движутся частицы, по мере же остывания их движение становится всё более медленным, и в случае с кристаллическими телами частицы постепенно всё ближе и ближе перемещаются к позициям, соответствующим узлам кристаллической решётки. В процессе остывания система приближается к состоянию, соответствующему энергетическому минимуму. В машине Больцмана таким энергетическим минимумом является состояние, при котором набор синаптических весов (включая смещения) и состояний нейронов находится в «полностью непротиворечивом состоянии» (когда состояния нейронов видимого слоя, установленные в результате инициализации сети, совпадают с их состояниями, рассчитанными на основе синаптических входов). Энергию системы создатели модели описывают при помощи следующей нехитрой формулы:

$E=-{\sum }_{i<j}^{}{w}_{ij}{s}_i{s}_j+{\sum }_i^{}{\theta }_i{s}_i$,

где w_ij — вес синапса, соединяющего нейроны i и j; s_i — состояние нейрона (0 или 1); θ — смещение. Условие i < j при суммировании нужно для того, чтобы исключить повторное суммирование для одних и тех же синапсов (поскольку синаптические связи в машине Больцмана полностью симметричны). Энергия суммируется для всего набора имеющихся у нас прецедентов. Процесс обучения начинается с точки, соответствующей случайному набору весов и некоторой величины температуры T. Затем на каждом шаге мы выбираем случайным образом новую точку в окрестностях текущей и рассчитываем величину энергии для неё. Если энергия в новой точке меньше, то мы переходим в неё со стопроцентной вероятностью. Если же величина энергии в новой точке больше или равна текущей, то мы переходим в неё или остаёмся в старой точке с некой вероятностью, зависящей от текущей температуры и энергии в старой и новой точках. Эта зависимость называется функцией вероятности принятия [acceptance probability function]. Можно использовать различные функции принятия, но классическая такова:

$P(E,E^{\text{'}},T)=e^{-\frac{E^{\text{'}}-E}{T}}$,

где P — вероятность перехода, E — энергия в текущей точке, E’ — энергия в новой точке, T — температура.

На следующем шаге мы уменьшаем величину T и повторяем процедуру, пока температура не достигнет нуля, а энергия — минимума.

Обученную машину Больцмана можно использовать так же, как и любой другой автокодировщик, — либо для расчёта латентного вектора для прецедента, либо для генерации нового прецедента на основе заданного (например, случайного) латентного вектора.

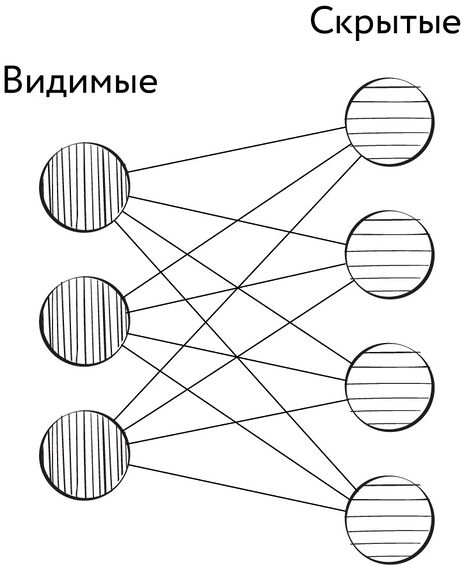
Ограниченная машина Больцмана, предложенная изначально в 1986 г. Полом Смоленским под названием Harmonium, представляет собой частный случай машины Больцмана, получаемый путём добавления следующего ограничения: синаптические связи могут связывать только скрытые нейроны с видимыми (но не скрытые со скрытыми или видимые с видимыми).

Рис. 111. Синаптические связи в ограниченной машине Больцмана

Завершённая в 1987 г. диссертация Лекуна, публикации Галлинари и его коллег, а также Бурлара и Кампа заложили основы применения автокодировщиков.

В 1990-е и начале 2000-х гг. исследования автокодировщиков продолжались. Например, в 1991 г. свет увидела работа Марка Крамера из MIT, в которой было показано преимущество автоэнкодеров (сам Крамер использовал термин «автоассоциативные нейронные сети» (Autoassociative Neural Networks)) над классическим методом главных компонент. В 1990-е и начале 2000-х гг. основным центром исследования автокодировщиков была группа Джеффри Хинтона в Торонто. В это время активно изучаются^, различные способы обучения таких сетей, позволяющие добиться наилучших результатов. Важным шагом вперёд становится появление глубоких сетей доверия — варианта ограниченной машины Больцмана с несколькими слоями скрытых нейронов (при этом допускаются связи между нейронами различных скрытых слоёв, но не внутри отдельного слоя). Для обучения таких сетей в начале 2000-х гг. в группе Хинтона применяли алгоритмы послойного обучения. Однако в целом можно сказать, что автокодировщики оставались в тени других нейросетевых моделей того времени (в первую очередь свёрточных и рекуррентных сетей). По всей видимости, в те годы многим исследователям казалось, что автокодировщики представляют главным образом теоретический интерес, а на практике могут применяться лишь в небольшом числе весьма специфических задач.

Резкий рост интереса к автоэнкодерам начался уже в 2010-е гг. В 2011 г. была опубликована революционная работа исследователей из группы Юргена Шмидхубера в лаборатории искусственного интеллекта швейцарского института IDSIA (Istituto Dalle Molle di Studi sull’Intelligenza Artificiale, Институт исследований искусственного интеллекта Далле Молле) под названием «Сгруппированные свёрточные автокодировщики для извлечения иерархических признаков» (Stacked Convolutional Auto-Encoders for Hierarchical Feature Extraction), в которой впервые описаны свёрточные автоэнкодеры [convolutional autoencoders], ставшие результатом комбинации автокодировщиков со свёрточными нейронными сетями. В свёрточном автоэнкодере роль кодировщика выполняет свёрточная сеть, а обратную ей роль декодера — развёрточная [deconvolutional].

В дальнейшем, по мере развития свёрточных нейронных сетей, совершенствовались и свёрточные автокодировщики. Также было придумано множество модификаций целевых функций, позволяющих улучшить результаты подобных моделей при решении различных задач. В целом за три последних десятилетия автокодировщики прошли большой путь — от теоретических моделей до гигантских нейронных сетей, предназначенных для обработки самых разных видов данных — от текстов до изображений и звуков.

Концепция кодировщиков и декодеров легла в основу многих важных моделей глубокого обучения. Фактически на её базе возникла целая подотрасль, получившая название «обучение представлениям» (или «обучение признакам») [representation learning] и занимающаяся изучением и разработкой техник, позволяющих системам машинного обучения автоматически находить представления, необходимые для выявления отдельных признаков или классификации данных. Благодаря обучению представлениям в наши дни активно развиваются методы машинного обучения с частичным привлечением учителя. К их числу относится, например, «контрастное обучение» [contrastive learning], о котором мы расскажем немного подробнее.

Контрастное обучение — это метод машинного обучения, используемый для изучения общих характеристик набора неразмеченных данных путём обучения модели тому, насколько похожи друг на друга его отдельные элементы (прецеденты). При этом контрастное обучение принято рассматривать как часть более широкой области, получившей название «метрическое обучение» [metric learning].

Представим себе маленького ребёнка, играющего в детский деревянный конструктор, в составе которого есть детали в форме куба, цилиндра, шара, прямоугольного параллелепипеда, тетраэдра и так далее. Ребёнок никогда не слышал этих слов, но в процессе игры его мозг способен изучить различные высокоуровневые признаки этих объектов: наличие или отсутствие плоских граней, их число, соотношения длин сторон и так далее. Благодаря этому позже, узнав, например, слово «куб», ребёнок сможет соотнести его сразу со всеми кубами, включая даже те, которые он раньше никогда не видел и не держал в руках.

Решая эту задачу при помощи автокодировщика, мы хотим добиться того, чтобы выучиваемые им представления (т. е. латентные векторы) обладали следующим свойством: для двух похожих предметов расстояние между соответствующими им векторами должно быть по возможности минимальным, в то время как расстояние между различающимися предметами должно быть по возможности максимальным. То есть мы, по сути, стремимся расположить соответствующие представлениям точки таким образом, чтобы границы между различными классами объектов были максимально «контрастными».

Однако по условию задачи у нас изначально нет метки класса как таковой. Ввиду этого исследователи применяют хитрый приём: каждый прецедент подвергается множеству трансформаций, которые не должны привести к смене метки целевого класса. Например, если мы имеем дело с изображениями, то к числу таких трансформаций могут относиться повороты, зеркальные отражения, размытие, добавление различных видов шума, изменение яркости, контраста, сдвиги цветов и так далее. При помощи таких трансформаций из одного изображения можно получить множество, составляющее отдельный псевдокласс. Теперь, имея полученный обогащённый набор данных, можно приступать к задаче обучения модели. В качестве целевой функции мы будем использовать такую функцию, которая будет максимизировать расстояние между представлениями прецедентов, относящихся к разным псевдоклассам, и минимизировать расстояние между представлениями, соответствующими прецедентам из одного и того же псевдокласса. В последние годы был разработан целый ряд разновидностей контрастного обучения. Например, можно составить обучающую выборку из пар прецедентов и обучать на ней сеть, состоящую из двух подсетей-кодировщиков с одинаковыми весами, выходы которых будут пропускаться через третью подсеть, вычисляющую расстояние между выходами двух первых подсетей. На выходе третья подсеть должна будет сделать предсказание — относятся прецеденты в паре к одному или тому же псевдоклассу или нет. Такой подход получил название «сиамских сетей» (поскольку веса сетей-кодировщиков идентичны, они являются как бы сиамскими близнецами). Вместо вычисления расстояний можно использовать и более хитрые способы оценки представлений, выучиваемых кодировщиками. В результате развития этой идеи в последние годы появилось множество интересных архитектур (MoCo, MoCo v2, SwAV, BYOL, SimCLR, SimCLR v2 и др.).

Остановимся для примера на одной из них. В 2021 г. целый ряд работ был посвящён новому подходу, получившему название «близнецы Барлоу» [Barlow twins]. Он был создан командой исследователей из компании Facebook под впечатлением от исследования нейрофизиолога Хораса Барлоу. В его статье, написанной ещё в 1961 г., была предложена смелая гипотеза о кодировании сенсорной информации в нервной системе, в соответствии с которой цель обработки сенсорной информации мозгом — избавиться от избыточности и перекодировать сигнал в код, компоненты которого будут статистически независимы. Для того чтобы оценить статистическую независимость представлений двух прецедентов, относящихся к одному псевдоклассу, создатели «близнецов Барлоу» заставляют сеть вычислить матрицу взаимной корреляции (кросс-корреляции) двух представлений. В идеальном случае главная диагональ этой матрицы должна быть заполнена единицами (соответствующие элементы двух представлений линейно зависимы, что означает, что представление оказалось инвариантным относительно внесённых искажений), а остальные элементы — нулями (отсутствует корреляция между всеми другими парами компонентов представления). Степень отклонения от этого идеального случая и есть функция потерь, которая в процессе обучения должна быть подвергнута минимизации. При этом второй компонент функции потерь (отличие от нуля недиагональных элементов матрицы) включается в неё с некоторым заданным весом, который можно настраивать. Такой подход позволяет при обучении обойтись без отрицательных примеров и хорошо работает с представлениями достаточно большой размерности. Почему это работает? Как и в случае других методов глубокого обучения, исследователи уже придумали несколько весьма остроумных объяснений наблюдаемому эффекту, отталкиваясь от метода «информационного бутылочного горлышка» [Information bottleneck method] Нафтали Тишби, критерия независимости Гильберта — Шмидта [Hilbert-Schmidt Independence Criterion]^, и других страшных слов и фамилий.

Обучение представлениям — одна из быстроразвивающихся областей глубокого обучения в наши дни, и не исключено, что в ближайшем будущем здесь нас ждёт ещё множество замечательных открытий.

Loading comments...