Перейти к содержанию

6.3.3.3 Революция word2vec

Материал из Охота на электроовец: Большая Книга Искусственного Интеллекта

Во второй половине 2000-х — начале 2010-х гг. под влиянием работ Бенджио и его коллег был опубликован ряд работ, в которых авторы предлагали различные системы построения универсальных словарных эмбеддингов для решения задач машинного обучения с частичным привлечением учителя [semi-supervised learning] в области обработки естественного языка.

Идея о том, что семантическую информацию о слове можно получить без привлечения учителя, на основе анализа больших неразмеченных наборов текстов, берёт своё начало ещё в XX в. На заре 1950-х гг. благодаря усилиям американского лингвиста Зеллига Харриса, уже упоминавшегося нами в качестве одного из учителей Хомского, приобрела популярность так называемая дистрибутивная гипотеза, которая сегодня обычно формулируется следующим образом: лингвистические единицы, встречающиеся в сходных контекстах, имеют близкие значения. Проще говоря, слова, которые используются и встречаются в одинаковых контекстах, как правило, имеют близкие значения[1]. В общем, Харрис, как можно заметить, вовсе не был активным противником корпусной лингвистики[2], в отличие от Хомского, который считал её пустой тратой времени[3]. Фактически гипотеза Харриса стала развитием идеи, высказанной в афористичной форме другим лингвистом — англичанином Джоном Фёрсом: «Слово характеризуется компанией, в которой оно встречается» [a word is characterized by the company it keeps][4]. В общем, в отношении слов, как и в отношении людей, в какой-то мере верна поговорка: «Скажи мне, кто твои друзья, и я скажу, кто ты». Возможно, Фёрс и не был первым мыслителем, высказавшим эту идею. Ещё в 1930-е гг. сходные суждения высказывал австрийский философ и логик Людвиг Витгенштейн[5]. Задолго до появления нейронных сетей лингвисты применяли метод дистрибутивного анализа, изучая распределения слов и символов в текстах, и даже (с середины XX в.) описывали семантику слов в виде контекстных векторов, в которых тому или иному смысловому признаку приписывались некоторые численные оценки. Возникла и развивалась целая область лингвистики, получившая название «дистрибутивная семантика». Её предметом стал анализ семантики элементов языка на основании их распределения в больших массивах лингвистических данных. Появление вычислительной техники, а затем и больших корпусов оцифрованных текстов вывело дистрибутивную семантику на новый уровень — позволило производить эксперименты и проверять гипотезы без использования трудоёмких ручных операций. Исследователями дистрибутивной семантики был разработан ряд инструментов, предназначенных для анализа больших корпусов текстов. Наиболее популярным из них стал Sketch Engine. Эта система была разработана компанией Lexical Computing Limited, созданной в результате сотрудничества лингвиста Адама Килгарриффа и Павла Рыхлого — специалиста в области информатики из Центра обработки естественного языка в Университете Масарика (Masaryk University). Sketch Engine позволяет среди прочего автоматически находить слова со сходной статистикой контекстов (формировать так называемый дистрибутивный тезаурус)[6]. Корпусными лингвистами были разработаны различные метрики для оценки близости значений слов и математические модели, предназначенные для получения нового знания о языке, позволявшие подтверждать или опровергать различные гипотезы при помощи статистических методов. Появление таких инструментов, как Sketch Engine, позволило лингвистам осуществлять массовую проверку различных гипотез, анализировать происходящие в языке диахронические[7] изменения, предоставило лексикографам возможность быстрой проверки соответствия словарных определений реальной практике употребления слов.

Дело оставалось за малым — придумать такой алгоритм, который мог бы проанализировать контексты, в которых каждое слово встречается в огромном текстовом корпусе, и построить для каждого слова некий семантический вектор, который содержал бы в себе всю необходимую смысловую информацию. Опираясь на такое представление, модели машинного обучения (например, нейронные сети) могли бы эффективно решать различные задачи, требующие понимания естественного языка.

В начале XXI в. был опубликован ряд работ, посвящённых попыткам создания подобного алгоритма.

Среди них можно отметить статьи[8], [9] Андрия Мниха — ещё одного аспиранта Джеффри Хинтона, Ронана Коллоберта и Джейсона Уэстона[10], а также соавторов Бенджио — Джозефа Туриана и Льва-Арье Ратинова[11]. Однако решительный прорыв удалось совершить только в 2013 г., когда группа исследователей из компании Google под руководством Томаша Миколова опубликовала работу под названием «Эффективное вычисление представлений слов в векторном пространстве» (Efficient Estimation of Word Representations in Vector Space)[12]. В конце того же года свет увидела вторая статья за авторством Миколова и его коллег под названием «Распределённые представления слов и фраз и их композиционность» (Distributed Representations of Words and Phrases and their Compositionality)[13], развивающая первое исследование и раскрывающая ряд новых деталей.

Помимо статей, была опубликована утилита для построения векторных представлений слов (word2vec, от word to vector — слово в вектор), а также сами наборы векторов для слов английского языка. На основе анализа поданного на вход большого текстового корпуса word2vec рассчитывает вектор признаков для каждого слова, встречающегося в корпусе, и создаёт на выходе словарь, включающий сами слова и наборы координат соответствующих им векторов.

«Под капотом» word2vec можно обнаружить сразу две нейросетевые модели, получившие названия «непрерывный мешок слов» (Continuous Bag of Words, CBOW) и «скипграмма» (Skip-gram). Обе эти модели являются прямыми наследницами модели Бенджио, поскольку получены из неё путём нескольких принципиальных доработок.

За прошедшее со времени исследований Бенджио и его коллег десятилетие появилась возможность обучать более «тяжёлые» модели с большим числом параметров. Создатели word2vec смогли увеличить длину контекста до десяти слов, а также использовать от 500 до 1000 нейронов в промежуточном (скрытом) слое сети. Однако этот прогресс был достигнут не только благодаря использованию нового поколения оборудования, но и ввиду применения методов для уменьшения количества параметров в выходном слое сети. Дело в том, что количество нейронов в выходном слое сети Бенджио равно количеству слов в словаре, и даже при сравнительно небольшом размере словаря, как это было в оригинальной работе Бенджио и его коллег, это становится проблемой. Ведь уже при словаре в 16 000 слов и 100 нейронах в скрытом слое мы получим 1,6 млн параметров, а что будет, если задействовать не игрушечный, а соответствующий реальному многообразию слов естественного языка словарь? Для реальных задач в области обработки естественного языка могут потребоваться словари в сотни тысяч или даже миллионы слов. В работе Миколова и его коллег использовался словарь размером в миллион слов, что при тысяче нейронов скрытого слоя даёт миллиард параметров на выходе сети. При размерности вектора признаков, равной 200, и длине контекста в десять слов общее число параметров сети будет равно 200 × 10 (входной слой) + 200 × 10 × 1000 (промежуточный слой) + 1000 × 1 000 000 (последний слой) = 1 002 002 000 — миллиарду с хвостиком. Как видно из этого расчёта, наибольшая часть параметров приходится на последний слой сети.

Миколов и его коллеги придумали, как можно уменьшить количество параметров в выходном слое сети, для чего ими было предложено два альтернативных метода: отрицательное семплирование [negative sampling] и иерархический softmax [hierarchical softmax].

Рассмотрим их подробнее.

Традиционно выходной слой нейронных сетей, используемых в задачах классификации с более чем двумя классами, применяет функцию softmax для нормализации выходных значений. Поскольку каждое выходное значение мы интерпретируем как вероятность принадлежности объекта одному из классов, то сумма выходных значений сети должна быть равна единице. Функция softmax является обобщением логистической функции для многомерного случая и рассчитывается по следующей нехитрой формуле:

f(xi)=exi∑jexj.

То есть фактически мы делим экспоненту каждого из выходов слоя на сумму экспонент всех таких выходов. Как несложно заметить, для вычисления этой функции нам нужны значения всех выходов слоя. Получается, что при обучении подобных сетей надо вычислить экспоненту для каждого из громадного числа выходов, что весьма затратно. Поэтому при использовании отрицательного семплирования мы отказываемся от нормализации выходов сети, а просто пропускаем каждый из выходов через логистическую функцию. При этом, разумеется, сумма выходов сети перестаёт быть строго равной единице, но, как выясняется, это не влияет на качество полученных векторов признаков.

Далее, вместо расчёта ошибок и последующего обновления весов для всех выходов сети мы выбираем для этого лишь их часть: выход, соответствующий истинной метке класса (т. е. слову, действительно встретившемуся в тексте), и несколько других отобранных выходов, для которых мы хотим, чтобы сеть выдавала 0 (так называемых отрицательных примеров, отсюда и название метода). В статье говорится, что для маленьких датасетов достаточно 5−20 отрицательных примеров, а для больших и вовсе 2–5. Таким образом, при использовании отрицательного семплирования обновлению на каждом шаге подвергается лишь крошечная доля синаптических весов модели.

Отрицательные примеры отбирают случайным образом, но с вероятностями, зависящими от частоты соответствующих им слов в используемом корпусе (т. е. часто встречающиеся слова имеют больший шанс оказаться выбранными как отрицательные примеры, чем редкие). В результате экспериментов Миколов и его коллеги пришли к выводу, что наилучшие результаты получаются при использовании вероятностей, пропорциональных частотам слов, возведённым в степень ¾. Такого рода константы (как и метод отрицательного семплирования) являются характерным примером экспериментальной алхимии в духе школы «грязнуль», которым в значительной мере пропитан весь современный коннекционизм.

Впрочем, прежде чем перейти к столь радикальным мерам, команда Миколова опробовала более математически строгий способ решения проблемы большого количества параметров в выходном слое, получивший название «иерархический softmax». Для этого выходной слой сети был реорганизован весьма оригинальным образом. Для начала словарь был представлен в виде двоичного дерева. Рассмотрим алгоритм, применявшийся для его построения.

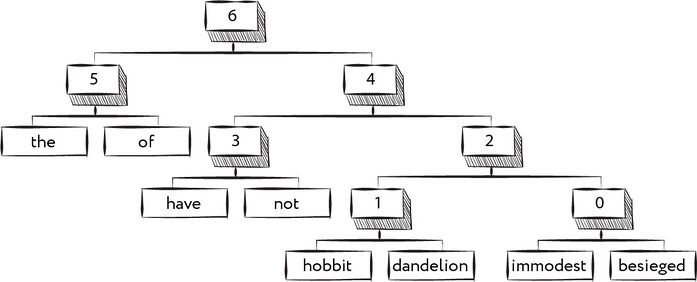
Рис. 129. Двоичное дерево, представляющее словарь

Предположим, что наш словарь содержит всего восемь слов: the, of, have, not, hobbit, dandelion, immodest и besieged. Для начала подсчитаем количество вхождений каждого из слов в наш корпус. Допустим, в итоге мы получили следующий набор пар вида (слово; число вхождений): (the; 123), (of; 119), (have; 61), (not; 57), (hobbit; 27), (dandelion; 25), (immodest; 22), (besieged; 19). Возьмём теперь две пары с самым маленьким числом вхождений, в нашем случае это будут пары (immodest; 22), (besieged; 19). Объединим эти пары в единый узел дерева, пусть это будет узел «0». Теперь удалим из списка объединённые нами пары и вместо них добавим пару, соответствующую вновь созданному узлу. В качестве числа вхождений будем использовать сумму соответствующих значений для объединённых нами пар. В результате мы получим следующий список: (the; 123), (of; 119), (have; 61), (not; 57), (hobbit; 27), (dandelion; 25), («0», 41). Будем повторять эту процедуру, пока в списке не останется единственная пара, соответствующая корню построенного двоичного дерева:

шаг 1: (the; 123), (of; 119), (have; 61), (not; 57), (hobbit; 27), (dandelion; 25), («0», 41)

шаг 2: (the; 123), (of; 119), (have; 61), (not; 57), («1», 52), («0», 41)

шаг 3: (the; 123), (of; 119), (have; 61), (not; 57), («2», 93)

шаг 4: (the; 123), (of; 119), («3», 118), («2», 93)

шаг 5: (the; 123), (of; 119), («4», 211)

шаг 6: («5»; 242), («4», 211)

шаг 7: («6»; 453)

Использованный нами алгоритм был разработан в 1952 г. и носит название «алгоритм Хаффмана», в честь его создателя Дэвида Хаффмана. Он относится к числу алгоритмов так называемого частотного кодирования и обычно применяется в задачах, связанных со сжатием данных. Дело в том, что дерево, построенное при помощи алгоритма Хаффмана, является визуализацией двоичного кода, позволяющего компактно представлять последовательности, состоящие из элементов, из которых было построено данное дерево. Двоичный код — это последовательность нулей и единиц. В случае дерева Хаффмана для кодирования каждого элемента мы будем использовать код, соответствующий пути, который следует пройти от корня дерева до нашего элемента. При этом 0 будет означать шаг влево, а 1 — шаг вправо. В нашем случае словам из словаря будут поставлены в соответствие следующие коды:

Слово Код
the 00
of 01
have 100
not 101
hobbit 1100
dandelion 1101
immodest 1110
besieged 1111

Идея кода Хаффмана заключается в том, что более часто встречающиеся элементы получат более короткие коды, что позволит минимизировать число бит, необходимое для хранения последовательности.

При использовании иерархической версии softmax выходной вектор сети имеет размерность, равную числу внутренних узлов дерева Хаффмана, построенного для используемого словаря. В нашем случае таких узлов семь («0», «1», …, «6»). Для каждого компонента вектора мы используем логистическую функцию активации, при этом сопоставление узлов и слов идёт следующим образом: значения в узлах меньше или равные 0,5 интерпретируются как шаги влево в них, а значения больше 0,5 — как шаги вправо. Например, слову hobbit будут соответствовать значения больше 0,5 у узлов «6» и «4» и значения меньше 0,5 у узлов «2» и «1» (здесь сумма компонентов выходного вектора вовсе не обязана быть равна единице). Кроме того, при каждом шаге мы будем обновлять веса только части выходов (узлов) — тех, через которые проходит путь в дереве, соответствующий правильной метке класса. При таком подходе обновления на каждом шаге обычно будут затрагивать не более чем log2N выходов сети, то есть при миллионе слов в словаре среднее число обновляемых выходов не будет превышать 20.

Миколов и его коллеги не были первыми исследователями, использовавшими двоичные деревья для кодирования слов на выходе нейронной сети, однако они были первыми, кто стал использовать для этой цели деревья Хаффмана.

Хотя в чистом виде иерархический softmax и проиграл отрицательному семплированию в экспериментах по точности, но благодаря применению алгоритмического трюка под названием «прореживание частых слов» (Subsampling of Frequent Words) ему удалось продемонстрировать наилучшие результаты по сравнению с другими методами[14].

Однако на этом эксперименты по сокращению вычислительной сложности модели не окончились. Следующая модель, «непрерывный мешок слов» (CBOW), лишилась скрытого слоя. В качестве контекста теперь использовалось восемь слов — четыре предшествующих тому слову, для которого строился прогноз, и четыре следующих в тексте за ним. Кроме того, если раньше на вход сети попадала конкатенация векторов признаков различных слов контекста, то теперь на вход поступал усреднённый вектор признаков для всех слов контекста. Именно из-за этой особенности модель и получила своё название, поскольку порядок слов контекста в ней игнорировался так же, как он игнорируется при использовании классического «мешка слов». Вторая модель, получившая название Skip-gram, решала обратную задачу, а именно: пыталась по одному слову предсказывать слова окружающего его контекста.

Благодаря относительной легковесности модели CBOW и Skip-gram оказались способны обучаться на гигантском корпусе Google News (около 6 млрд слов) при размере словаря в миллион слов. При использовании одного CPU на одну эпоху обучения уходило при этом не более суток.

Миколов и его коллеги опробовали различные размерности эмбеддингов (размерностью эмбеддингов часто для простоты называют число компонентов векторов признаков) — 50, 100, 300, 600 и даже 1000. Обучив несколько моделей, авторы исследования сравнили свойства полученных векторов с векторами, построенными в экспериментах других исследователей, а также с векторами из более ранней работы[15] Миколова. Дело в том, что ещё за год до рассматриваемых нами исследований Миколов предложил усовершенствовать сеть Бенджио, сделав её рекуррентной, чтобы в дополнение к поступающему на вход на каждом шаге вектору, соответствующему очередному слову текста, сеть использовала также информацию из своих предыдущих состояний. Для обозначения модели Бенджио (в том числе её различных усовершенствованных версий) Миколов и его коллеги используют аббревиатуру NNLM (Neural network language mode, Нейросетевая языковая модель), а для обозначения её рекуррентной версии — аббревиатуру RNNLM (Recurrent neural network language model, Рекуррентная нейросетевая языковая модель).

Для оценки качества полученных векторов авторы предыдущих исследований обычно использовали наборы слов. Для каждого слова из набора обычно рассматривался список слов, векторы которых по некоторой метрике расстояния были ближайшими к вектору исходного слова. В качестве метрики обычно использовалось косинусное расстояние, то есть разница между косинусами углов двух векторов.

Весьма занимателен вопрос о том, почему авторы word2vec использовали косинусное расстояние, а, например, не обычное евклидово. Дело в том, что косинусное расстояние игнорирует длину векторов, то есть если мы умножим любой из векторов, для которых рассчитывается расстояние, на некоторый скаляр, то косинусное расстояние между этими векторами не изменится. Именно поэтому косинусное расстояние часто используется в ситуациях, когда компонентой вектора является, например, число вхождений слова в некоторое множество документов; как раз такие векторы применяются в латентном семантическом анализе. Не исключено, что Миколов и его коллеги просто взяли привычную метрику, по крайней мере в их статьях нет объяснения использованию именно косинусного расстояния. Впрочем, более поздние исследования[16], [17], [18] показали, что длина вектора признаков слова в word2vec связана с частотой слова, поэтому при использовании евклидова расстояния синонимы, значительно разнящиеся по числу вхождений в обучающую выборку, могут оказаться достаточно далёкими друг от друга. Использование косинусного расстояния позволяет избегать таких ситуаций.

Хотя CBOW и Skip-gram, как выяснили Миколов и коллеги, хорошо отыскивают синонимы, объективно сравнить качество различных наборов векторов при решении этой задачи довольно сложно. Оценка степени семантической близости слов в ряде случаев сильно зависит от оценщика, поэтому Миколов и его коллеги поставили во главу угла обнаруженное ими интересное свойство вычисленных моделями векторов. Наблюдения исследователей показали, что отношения между векторами отражают различные семантические отношения между словами. Мы знаем, например, что слово «большой» относится к слову «больше» таким же образом, как слово «маленький» относится к слову «меньше», а слово «Москва» относится к слову «Россия» так же, как слово «Рим» относится к слову «Италия». Выяснилось, что если, например, из вектора, соответствующего слову «большой», вычесть вектор, соответствующий слову «больше», то результат будет близок к вектору, полученному путём вычитания из вектора слова «маленький» вектора слова «меньше». Благодаря этому свойству можно использовать полученные векторы для поиска ответов на вопросы вида «Какое слово так же относится к слову A, как слово X относится к слову Y?». Для этого нужно вычислить вектор B = A + X − Y и найти среди имеющихся векторов такой, который будет ближе всего к B (за исключением векторов, содержащихся в самом вопросе: A, X и Y).

Конечно, и такой подход в полной мере не исключает влияния субъективного фактора. Например, у ответов могут существовать синонимы. Но всё-таки такой способ выглядит гораздо более объективным, тем более что в ряде случаев тесты при его использовании можно создавать автоматически, что и сделали в своей работе Миколов и его коллеги. В частности, они использовали данные о столицах стран мира и штатов США, названия валют для стран, словарь антонимов, таблицы с разными формами слов и так далее. Используя эти наборы данных, можно было оценить, насколько успешно полученные наборы векторов способны давать ответ на вопросы типа «Какое слово относится к слову „Россия“ так же, как слово „доллар“ относится к слову „США“?» или «Какое слово относится к слову „дорогой“ так же, как слово „низкий“ относится к слову „высокий“?».

Миколов и его коллеги разделили все вопросы на две группы: семантические (например, нахождение страны по столице) и синтаксические (вопросы, в которых необходимо было подобрать близкие по форме слова: «быстро» — «быстрый»). Всего в тестовый набор было включено 8869 семантических и 10 675 синтаксических вопросов. На данной выборке модель Skip-gram с размерностью вектора признаков 300 продемонстрировала точность 53,3% (50,0% для семантических и 55,9% для синтаксических вопросов). Немного отстала от неё усовершенствованная версия модели NNLM с размерностью вектора признаков 100 — общая точность 50,8% (34,2 и 64,5% для семантических и синтаксических вопросов соответственно). Ранее же, при использовании векторов из более ранних работ других исследовательских групп, точность ответов на подобные вопросы не превышала 12,3%[19].

Появление векторов, созданных при помощи моделей Миколова и его коллег, означало настоящий прорыв в «понимании» естественного языка моделями машинного обучения. При этом главная заслуга создателей word2vec состояла не в том, что они улучшили качество работы моделей, а в том, что они, собрав все лучшие на тот момент достижения предшественников, создали прикладную методологию и подарили всем новый мощный инструмент для решения задач в области обработки естественного языка.

Интересно, что в 2020 г., спустя семь лет после выхода word2vec, исследователи из компании Bloomberg обнаружили[20], [21], что в оригинальной реализации word2vec (конкретно — в алгоритме CBOW) содержится ошибка, приводящая к снижению эффективности работы этого алгоритма. Хотя в 2020 г. мало кто в индустрии разрабатывает модели на основе word2vec (с тех пор появилось множество более совершенных моделей), но в эксплуатации в наши дни до сих пор наверняка остаётся ряд систем, использующих построенные при его помощи наборы эмбеддингов.

Словарные эмбеддинги нашли применение далеко за пределами сферы искусственного интеллекта. В наши дни их используют при решении самых разных задач в области лингвистики и семантики. Кроме того, для них нашлось применение и в сфере когнитивной психологии — как выяснилось, словарные эмбеддинги можно использовать для прогнозирования человеческого восприятия и оценок в таких разнообразных областях, как социальное познание[22], поведение людей в отношении вопросов здоровья, восприятие риска, организационное поведение[23] и маркетинг[24].

  1. ↑ Harris Z. (1954). Distributional structure / Word, Vol. 10, Iss. 23, pp. 146—162 // https://doi.org/10.1080/00437956.1954.11659520
  2. ↑ * Корпусная лингвистика — раздел языкознания, занимающийся разработкой, созданием и использованием текстовых корпусов.
  3. ↑ Wallis S. (2016). Why Chomsky was Wrong About Corpus Linguistics / corp.ling.stats: statistics for corpus linguists, November 2, 2016 // https://corplingstats.wordpress.com/2016/11/02/why-chomsky-was-wrong/
  4. ↑ Firth J. R. (1957). A synopsis of linguistic theory 1930-1955 // https://books.google.ru/books?id=T8LDtgAACAAJ
  5. ↑ Maruyama Y. (2019). Quantum Physics and Cognitive Science from a Wittgensteinian Perspective: Bohr’s Classicism, Chomsky’s Universalism, and Bell’s Contextualism / Wuppuluri S., da Costa N. (2019). WITTGENSTEINIAN (adj.). The Frontiers Collection. Springer, Cham // https://doi.org/10.1007/978-3-030-27569-3_20
  6. ↑ Kilgarriff A., Baisa V., Bušta J., Jakubíček M., Kovář V., Michelfeit J., Rychlý P., Suchomel V. (2014). The Sketch Engine: ten years on / Lexicography, Vol. 1, Iss. 1, pp. 7–36 // https://doi.org/10.1007/s40607-014-0009-9
  7. ↑ * Диахрония (от греч. δια — через, сквозь и χρονος — время) — рассмотрение исторического развития языковых явлений и языковой системы как предмета лингвистического исследования. Противопоставляется синхронии (от греч. συν — совместно и χρονος — время) — рассмотрение состояния языка как установившейся системы в определённый момент времени.
  8. ↑ Mnih A., Hinton G. E. (2009). A scalable hierarchical distributed language model / Advances in neural information processing systems, Vol. 21, pp. 1081—1088 // https://papers.nips.cc/paper/3583-a-scalable-hierarchical-distributed-language-model
  9. ↑ Mnih A., Teh Y. W. (2012). A fast and simple algorithm for training neural probabilistic language models // Proceedings of the 29th International Coference on International Conference on Machine Learning, pp. 419—426 // https://arxiv.org/abs/1206.6426
  10. ↑ Collobert R., Weston J. (2008). A unified architecture for natural language processing: deep neural networks with multitask learning / Proceedings of the 25th international conference on Machine learning, pp. 160—167 // https://doi.org/10.1145/1390156.1390177
  11. ↑ Turian J., Ratinov L., Bengio Y. (2010). Word representations: a simple and general method for semi-supervised learning / Proceedings of the 48th Annual Meeting of the Association for Computational Linguistics, pp. 384—394 // https://dl.acm.org/doi/10.5555/1858681.1858721
  12. ↑ Mikolov T., Chen K., Corrado G., Dean J. (2013). Efficient Estimation of Word Representations in Vector Space / International Conference on Learning Representations (ICLR-2013) // https://arxiv.org/abs/1301.3781
  13. ↑ Mikolov T., Sutskever I., Chen K., Corrado G., Dean J. (2013). Distributed Representations of Words and Phrases and their Compositionality / Proceedings of the 26th International Conference on Neural Information Processing Systems, Vol. 2, pp. 3111—3119 // https://papers.nips.cc/paper/5021-distributed-representations-of-words-and-phrases-and-their-compositionality.pdf
  14. ↑ Mikolov T., Sutskever I., Chen K., Corrado G., Dean J. (2013). Distributed Representations of Words and Phrases and their Compositionality / Proceedings of the 26th International Conference on Neural Information Processing Systems, Vol. 2, pp. 3111—3119 // https://papers.nips.cc/paper/5021-distributed-representations-of-words-and-phrases-and-their-compositionality.pdf
  15. ↑ Mikolov T., Kombrink S., Deoras A., Burget L, Černocký J. (2011). RNNLM — Recurrent Neural Network Language Modeling Toolkit / Proceedings of IEEE Automatic Speech Recognition and Understanding Workshop, 2011, pp. 1—4 // https://www.fit.vut.cz/research/publication/10087/.en
  16. ↑ Wilson B., Schakel A. M. J. (2015). Controlled Experiments for Word Embeddings // https://arxiv.org/abs/1510.02675
  17. ↑ Rajasekharan A. (2017). How does word2vec work? Can someone walk through a specific example? / Quora // https://www.quora.com/How-does-word2vec-work-Can-someone-walk-through-a-specific-example/answer/Ajit-Rajasekharan
  18. ↑ Gong C., He D., Tan X., Qin T., Wang L., Liu T.-Y. (2020). FRAGE: Frequency-Agnostic Word Representation // https://arxiv.org/abs/1809.06858
  19. ↑ Mikolov T., Chen K., Corrado G., Dean J. (2013). Efficient Estimation of Word Representations in Vector Space / International Conference on Learning Representations (ICLR-2013) // https://arxiv.org/abs/1301.3781
  20. ↑ İrsoy O., Benton A., Stratos K. (2020). kōan: A Corrected CBOW Implementation // https://arxiv.org/abs/2012.15332
  21. ↑ Сапунов Г. (2021). kōan: A Corrected CBOW Implementation (Ozan İrsoy, Adrian Benton, Karl Stratos) / gonzo-обзоры ML статей, Jan 19, 2021 // https://t.me/gonzo_ML/452
  22. ↑ * Социальное познание (англ. social cognition) — процесс познания одного человека другим, одна из сфер, изучаемых социальной психологией, которая исследует механизмы хранения, переработки и использования человеком информации о других людях и социальных ситуациях.
  23. ↑ ** Организационное поведение (англ. organizational behavior) — научная дисциплина, занимающаяся исследованием поведения людей в организациях.
  24. ↑ Richie R., Zou W., Bhatia S., Vazire S. (2019). Predicting High-Level Human Judgment Across Diverse Behavioral Domains / Psychology, Vol. 5, Iss. 1, p. 50 // https://doi.org/10.1525/collabra.282
Loading comments...
Источник — http://wiki.markoff.science/index.php?title=6.3.3.3_Революция_word2vec&oldid=1227