6.3.3.5 Вторая революция в NLP: трансформеры

Список моделей внимания можно продолжать ещё очень долго. Были изобретены латентное [latent] и активное [active] внимание, гауссовское [Gaussian] внимание, свёрточные нейронные сети на базе внимания (Attention Based Convolutional Neural Network, ABCNN), разложимая модель внимания [Decomposable Attention Model], областное внимание [Area Attention] и даже нейросетевой трансдьюсер (преобразователь) для онлайн-внимания [Neural Transducer for Online Attention]. Из описаний различных моделей на основе внимания и полученных при их помощи результатов можно было бы составить отдельную книгу, но здесь мы подробно остановимся лишь на одной из них, тем более что ей было суждено положить начало второй коннекционистской революции в области обработки естественного языка. Эта модель называется «трансформер» [transformer]. Она была представлена научному сообществу в 2017 г. в статье с программным названием «Внимание — это всё, что вам нужно» (Attention Is All You Need), написанной группой исследователей из Google Brain и Google Research.

Как часто бывает, некоторые идеи, положенные в основу трансформера, можно найти в работах^{, ,} , написанных в начале 1990-х годов Юргеном Шмидхубером. Тип внимания, положенный в основу трансформера, называется особенно страшно — «многоголовое внутреннее внимание» [multi-headed self-attention]. Разумеется, по-русски так его никто не называет, вместо этого отечественные специалисты просто используют термин в его английском варианте.

Одна из проблем рекуррентных сетей заключается в том, что при их вычислении трудно добиться эффективного параллелизма. Действительно, для того чтобы вычислить следующее состояние сети, необходимо получить результат вычисления предыдущего состояния — сама природа рекуррентной сети последовательна, поэтому максимум, что можно сделать, это вычислять параллельно результаты для разных последовательностей либо выполнять параллельные вычисления в пределах одного состояния рекуррентной сети, однако оба этих подхода обычно не позволяют в полной мере использовать вычислительный потенциал тензорных процессоров. Нельзя ли вообще отказаться от рекуррентной сети в пользу нерекуррентной архитектуры, сохранив при этом механизм внимания, показавший свою эффективность? Оказывается, можно (именно на это ненавязчиво указывает нам заголовок статьи исследователей из Google).

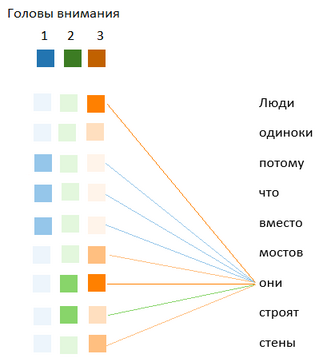
Рассмотрим для примера предложение: «Люди одиноки, потому что вместо мостов они строят стены». Кто такие в данном случае «они»? Человек, прочитавший это предложение, без особого труда понимает, что в данном случае слово «они» относится к слову «люди». Можно сказать, что у нас в голове возникает представление о наличии определённого отношения (в данном случае — тождества) между словами «они» и «люди». Другое отношение связывает слова «они» и «строят», а также «люди» и «строят» — это отношения вида «A выполняет действие B». И так далее — слова в высказывании связаны определёнными отношениями. Идея multi-headed self-attention заключается в том, чтобы для разных типов отношений (за каждый из них отвечает отдельная «голова» сети внимания, так же как в свёрточной сети за каждый выявляемый слоем свёртки признак отвечает отдельный набор весов для свёрточного ядра) рассчитать матрицу выравниваний, то есть для каждой пары слов в предложении выяснить, в какой мере выражено для неё данное отношение.

На рисунке для всех слов предложения показаны отношения со словом «они» у разных «голов внимания» (обозначенных синим, зелёным и оранжевым цветом), насыщенность цвета показывает выраженность отношения. Пример условный, для упрощения показаны только три «головы», а не восемь.

Рис. 131. Условный пример, показывающий отношения со словом «они»
для разных «голов внимания»

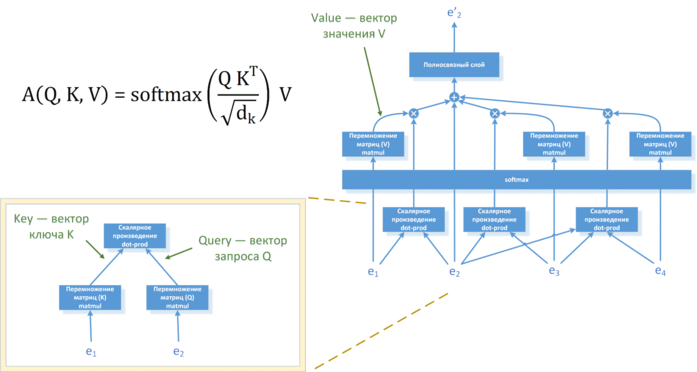
Для вычисления матрицы выравниваний в трансформере используется довольно красивая матричная операция, имитирующая извлечение значения из таблицы по ключу. Так же как и в случае «обычного» внимания, каждый из векторов эмбеддингов слов (которые являются в нашем случае аналогами состояний кодировщика) при помощи трёх проекций превращается в три новых вектора одинаковой размерности: вектор запроса Q (от query), вектор ключа K (от key) и вектор значения V (от value). После этого создаётся матрица, элементы которой будут показывать «отношения» между различными словами предложения (эту матрицу называют «матрицей внимания» [attention matrix]). Для этого элемент матрицы с индексами i и j вычисляется как скалярное произведение вектора запроса Q_i и вектора ключа K_j. Далее каждый элемент этой матрицы делится на квадратный корень из размерности вектора ключа K, а затем результат построчно пропускается через softmax-слой (тем самым производится нормализация коэффициентов, чтобы для каждой строки матрицы они в сумме давали единицу).

Далее для каждого слова предложения все векторы значений V умножаются на коэффициенты соответствующей этому слову строки из матрицы выравниваний и складываются, тем самым формируя некий итоговый вектор значений V. Таким образом, в нём будут хорошо учтены слова, имеющие определённые «отношения» с рассматриваемым словом, а иные слова, напротив, будут учтены слабо. Это и будет выходом такой подсети для данного слова предложения.

Схема данных операций приводится ниже, для сложения векторов значений V используются двухслойные полносвязные подсети, вычисление которых может осуществляться параллельно.

Рис. 132. Схема вычисления матрицы выравниваний в трансформере

На выходе подсетей возникает матрица той же размерности, что и на входе сети внимания. Однако такой выход у нас имеется для каждой из «голов внимания». Поэтому полученные матрицы мы склеиваем (конкатенируем) друг с другом, а затем превращаем в матрицу исходной размерности при помощи слоя проекции. Именно поэтому модель и называют трансформером — она трансформирует полученные на вход данные, не меняя их размерности. Благодаря этому свойству описанные нами блоки кодировщиков можно укладывать подобно стопке блинов — выходы одного блока становятся входами следующего. Для борьбы с исчезающими градиентами используются, как и в свёрточных сетях, перепрыгивающие связи.

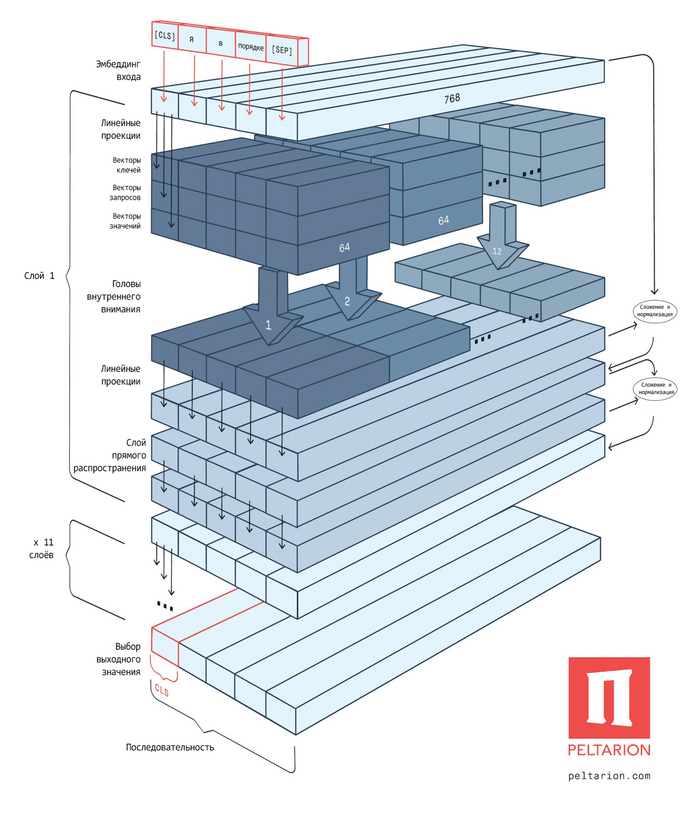
Рис. 133. Архитектура нейросетевой модели BERT, основанной на блоках трансформера.
CLS — специальный символ, добавляемый в начало каждого примера, SEP — специальный токен-разделитель. Каждому токену входной последовательности соответствует вектор эмбеддинга размерностью 768

Блок декодера в трансформерах устроен аналогичным образом за той лишь существенной разницей, что он имеет два входа: на один подаётся выход кодировщика, на второй — выход сети внимания, применённой к уже известной части выходной последовательности (этот тип внимания называется «многоголовым вниманием с маской» [masked multi-head attention], маска используется для исключения неизвестных на данный момент частей выходной последовательности).

Ещё одним интересным трюком, использованным в оригинальном трансформере, является применение так называемого позиционного кодирования. Дело в том, что сам по себе трансформер, подобно свёрточным сетям, теряет информацию о порядке следования слов, поэтому эту информацию следует добавлять к векторам эмбеддинга. Можно было бы добавить, например, порядковый номер слова в качестве ещё одной компоненты в эти векторы, но на практике лучше работают более хитрые способы. В оригинальной версии трансформера вычисляют так называемую матрицу позиционного кодирования [positional encoding] размером W × n, где W — размерность вектора эмбеддинга слова, а n — максимальное количество слов в обрабатываемом моделью тексте. В нечётные строки этой матрицы записываются значения, равные $\sin \left(\frac{j}{10000^{i/n}}\right)$, а в чётные — равные $\cos \left(\frac{j}{10000^{(i-1)/n}}\right)$, где i — номер строки, а j — номер столбца. Значения в каждом столбце матрицы напоминают показания причудливых часов, оснащённых множеством стрелок, причём у каждой следующей стрелки период обращения немного больше, чем у предыдущей. Применение нескольких временных шкал позволяет с лёгкостью обнаруживать в последовательности периодические явления с разной длиной периода. Затем матрицу позиционного кодирования складывают с матрицей, составленной из векторов эмбеддинга (эти матрицы имеют одинаковую размерность), и подают на вход блока внимания. Таким образом, вектор эмбеддинга для токена теперь включает информацию о позиции токена в обрабатываемой последовательности. Этот подход сегодня обычно называют «синусоидальным позиционным кодированием» [sinusoidal position encoding], а в целом методы, в которых векторы, соответствующие каждому из токенов, дополняются информацией об абсолютной позиции токена в обрабатываемой последовательности, называют «абсолютным позиционным кодированием» (Absolute positional encoding, APE).

Авторы оригинальной версии трансформера также исследовали подход, при котором модель сама выучивала матрицу позиционного кодирования. Каждому порядковому номеру токена в последовательности сопоставляется вектор, который на старте обучения инициализируется случайными значениями. Затем векторы эмбеддингов выучиваются одновременно с остальными параметрами сети, что позволяет в процессе обучения подстроить эмбеддинги так, чтобы они сочетались с временно́й компонентой наиболее полезным для модели образом. Такие эмбеддинги называют «абсолютными позиционными» (Absolute Positional Embeddings), а замена слова encoding на embedding подчёркивает особенность применяемого механизма (однако совпадение аббревиатур нередко служит источником непонимания для начинающих).

Обе версии трансформера показали в экспериментах примерно одинаковые результаты, поэтому авторы остановились на версии с синусоидальным кодированием, так как очевидным недостатком второго способа является то, что обученная модель будет способна работать только с последовательностями, длина которых не превышает количества выученных векторов позиционного эмбеддинга. Это, впрочем, не остановило создателей более поздних моделей на основе трансформерной архитектуры, например популярной и по сей день модели BERT (Bidirectional Encoder Representations from Transformers, Двунаправленный кодировщик представлений на основе трансформеров), в которой для кодирования позиционной информации используются именно абсолютные позиционные эмбеддинги.

Для того чтобы решить проблему с обработкой длинных последовательностей, исследователи из Google изобрели альтернативный способ кодирования позиции, который получил название «относительных позиционных эмбеддингов» (Relative Position Embeddings, RPE). Вместо того чтобы опираться на абсолютную позицию токенов, они используют расстояние между токенами (при этом если оно превышает максимальное значение, то считается равным ему) и выучивают векторы эмбеддингов, соответствующие этой относительной позиции. Эти векторы затем используются при расчёте матрицы внимания «на лету», поскольку каждой из её ячеек соответствуют конкретные позиции токенов входной последовательности. Способы учёта относительной позиционной информации при расчёте матрицы внимания могут различаться в зависимости от конкретной реализации. В первой работе, посвящённой позиционному кодированию, векторы эмбеддингов относительной позиции складываются с матрицей ключей (K) и с матрицей значений (V). Позже было показано, что можно ограничиться лишь сложением с матрицей ключей (K).

В современных трансформерных моделях обычно используются и более изощрённые способы позиционного кодирования — такие, например, как ротационные позиционные эмбеддинги (Rotational Position Embeddings, RoPE), экстраполируемые позиционные эмбеддинги (Extrapolatable Position Embeddings, xPos) или внимание с линейными смещениями (Attention with Linear Biases, ALiBi). Более того, некоторые исследования показывают, что трансформерные модели могут иногда работать и вовсе без позиционного кодирования.

Благодаря пригодности к эффективной параллелизации многослойные трансформеры быстро стали лидерами в самых разных задачах, причём не только в области обработки естественного языка, но и в других, связанных с обработкой последовательностей, вне зависимости от их природы. Музыка, записанная в виде последовательности нот, человеческая речь, представленная в виде последовательностей амплитуд звуковых волн, программный код, химические формулы, изображения, представленные в виде последовательностей пикселей, и даже последовательности действий в компьютерной игре — всё это может обрабатываться при помощи трансформеров.

Последующее переосмысление изначальной архитектуры привело к появлению трёх важных классов трансформерных сетей: сетей, основанных только на кодирующих блоках трансформера (энкодерные архитектуры), сетей, основанных только на декодирующих блоках (декодерные архитектуры), и архитектуры типа «кодировщик — декодер», использующие, подобно оригинальному трансформеру, оба типа блоков.

Энкодерные архитектуры чаще всего применяются в задачах, связанных с классификацией и поиском последовательностей. К их числу относятся, например, уже упоминавшаяся нами модель BERT и её наследники — ALBERT, RoBERTa и так далее.

Сама идея кодирования блока текста в вектор фиксированного размера, который можно использовать в задачах классификации или оценки семантической близости, значительно старше трансформеров — мы уже говорили об этом ранее. Благодаря комбинации векторных вложений с LSTM-сетями были созданы такие модели, как CoVe, ELMo, ULMFiT, позволившие заметно улучшить результаты методов, использовавших простые способы комбинации векторов отдельных слов (уже упоминавшийся нами dov2vec). Но с появлением BERT и других трансформерных кодировщиков подход с векторизацией текстов при помощи нейронных сетей приобрёл действительно широкую популярность.

Декодерные архитектуры более популярны в задачах генерации. Именно к этому классу относятся генеративные монстры GPT, GPT-2, GPT-3 и так далее от OpenAI, о которых мы поговорим несколько позже.

Сети типа «кодировщик — декодер» (T5 и др.) могут использоваться в самых разных задачах, и, хотя обычно они более затратны с вычислительной точки зрения, именно при их помощи удалось получить рекордные результаты во многих задачах, связанных с обработкой естественного языка.

Модели на основе трансформеров задали новую планку в качестве машинного перевода, сентимент-анализа (анализ тональности высказываний), языковом моделировании, диалоговых системах. Уровень «понимания» естественного языка, демонстрируемый этими моделями, существенно превосходит «способности» моделей предыдущего поколения.

Для оценки способности модели понимать естественный язык можно использовать тесты на понимание прочитанного. В английском языке для этого предназначен раздел «Чтение» (Reading) теста SAT (Scholastic Assessment Test/Scholastic Aptitude Test, Академический оценочный тест, стандартизованный тест, применяемый для оценки способностей абитуриентов при приёме в высшие учебные заведения в США, аналог российского ЕГЭ). На данном тесте основан крупнейший общедоступный ресурс для сравнения моделей — набор данных RACE (Large-scale ReAding Comprehension Dataset From Examinations, Крупномасштабный набор данных с экзаменов для понимания прочитанного), созданный в 2017 г. и содержащий около 28 000 отрывков и около 100 000 вопросов, сформулированных преподавателями английского языка. При случайном выборе ответов точность составляет 25%, а точность, показанная людьми (пользователями платформы Amazon Mechanical Turk) после отбрасывания вопросов с неоднозначным ответом и вопросов без правильного ответа, — около 95%.

Успехи систем в области обработки естественного языка на данном наборе хорошо отражают достижения последних лет. Модель предыдущего поколения Gated-Attention Reader показала на данном наборе точность в 46%, модель BERT — 72%, усовершенствованные версии модели BERT — XLNet и RoBERTa — улучшили точность до 82–83%, а самая новая версия модели BERT — ALBERT-xxlarge — смогла показать на данном наборе рекордную точность в 89,4%.

Loading comments...